题目内容
已知数列 ,
, 满足
满足 ,
, ,
, ,数列
,数列 的前
的前 项和为
项和为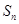 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: ;
;
(3)求证:当 时,
时, .
.
(1)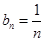 ,(2)详见解析,(3)详见解析.
,(2)详见解析,(3)详见解析.
解析试题分析:(1)求数列 的通项公式,需先探究数列
的通项公式,需先探究数列 的递推关系,由
的递推关系,由 ,得
,得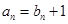 ,代入
,代入 ,得
,得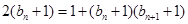 ,∴
,∴ ,从而有
,从而有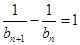 ,∵
,∵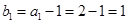 ,∴
,∴ 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴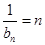 ,即
,即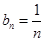 .(2)∵
.(2)∵ ,∴
,∴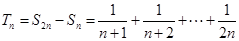 ,
, ,∴
,∴ .(3)∵
.(3)∵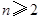 ,∴
,∴

 .由(2)知
.由(2)知 ,∴
,∴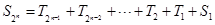
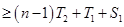
∵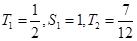 ,所以
,所以
解:(1)由 ,得
,得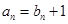 ,代入
,代入 ,
,
得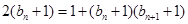 ,
,
∴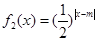
 ,从而有
,从而有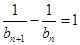 ,
,
∵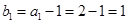 ,
,
∴ 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴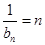 ,即
,即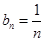 .
.
(2)∵ ,∴
,∴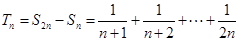 ,
,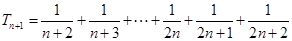 ,
,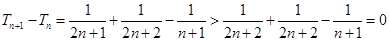 ,
,
∴ .
.
(3)∵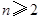 ,
,
∴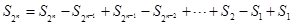

 .
.
由(2)知 ,∵
,∵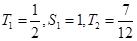 ,
,
∴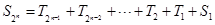
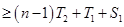
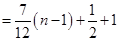
 .
.
考点:求数列通项,数列不等式

练习册系列答案
相关题目
 =p(p为正常数,n∈N+),则称{an}为“等方比数列”.
=p(p为正常数,n∈N+),则称{an}为“等方比数列”. 前
前 项和
项和 ,
,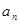 ;(2)若它的第
;(2)若它的第 项满足
项满足 ,求
,求 满足
满足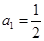 ,
, .
. 的值,由此猜测
的值,由此猜测 .
. ,an=
,an= (
(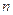 为正整数),
为正整数), ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn, 的首项
的首项 ,公差
,公差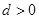 ,且第
,且第 项、第
项、第 项、第
项、第 项分别是等比数列
项分别是等比数列 的第
的第 项、第
项、第 项.
项. 对任意
对任意 ,均有
,均有 成立.
成立. ; ②求
; ②求 .
. 为等差数列,
为等差数列, ,其前n项和为
,其前n项和为 ,若
,若 ,
, 值.
值. 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数. 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列; 项积为
项积为 ,即
,即 ,求
,求 ;
; ,求数列
,求数列 的前
的前 ,并求使
,并求使 的
的