题目内容

已知tan(α-β)=，tanβ=-，且α,β∈(0,π)，求2α-β的值.

解：∵2α-β=2(α-β)+β,tan(α-β)= ，

∴tan2(α-β)=.

从而tan(2α-β)=tan［2(α-β)+β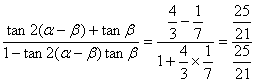］==1.

又∵tanα=tan［(α-β)+β］=＜1,

且0＜α＜π，∴0＜α＜.

∴0＜2α＜.

又tanβ=-＜0，且β∈(0,π)，

∴＜β＜π,-π＜-β＜-.∴-π＜2α-β＜0.

∴2α-β=-

练习册系列答案
相关题目
已知tanα=-
1
3
，cosβ=
5
5
，α，β∈（0，π）
（1）求tan（α+β）的值；
（2）求函数f(x)=
2
sin(x-α)+cos(x+β)的最大值．
已知tanα，tanβ为方程x2-3x-3=0两根．
（1）求tan（α+β）的值；
（2）求sin2（α+β）-3sin（2α+2β）-3cos2（α+β）的值．
已知tan(θ+
π
4
)=-3，则sin2θ+sinθcosθ-2cos2θ=（　　）
A、-
4
3
B、
5
4
C、-
3
4
D、
4
5
已知tan
α
2
=2，
求；（1）tan(α+
π
4
)的值；
（2）
6sinα+cosα
3sinα-2cosα
的值；
（3）3sin2α+4sinαcosα+5cos2α的值．
（1）已知sinα-cosα=
17
13
，α∈（0，π），求tanα的值；
（2）已知tanα=2，求
2sinα-cosα
sinα+3cosα
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网