题目内容
已知椭圆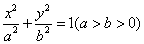 的右焦点为
的右焦点为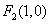 ,点
,点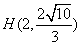 在椭圆上.
在椭圆上.
 (1)求椭圆的方程;
(1)求椭圆的方程;
(2)点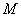 在圆
在圆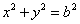 上,且
上,且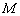 在第一象限,过
在第一象限,过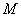 作圆
作圆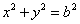 的切线交椭圆于
的切线交椭圆于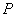 ,
,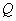 两点,问:△
两点,问:△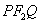 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由.
:
(1)『解法1』:
(Ⅰ)由题意,得 ,
,
解得
∴椭圆方程为 .
.
『解法2』:
 右焦点为
右焦点为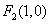 ,
,

左焦点为 ,点
,点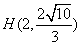 在椭圆上
在椭圆上

所以 ,
,
所以椭圆方程为
(2)『解法1』:
由题意,设 的方程为
的方程为
∵ 与圆
与圆 相切
相切
∴ ,即
,即
由 ,得
,得
设 ,则
,则 ,
,
∴





又


∴
∴ (定值)
(定值)
『解法2』:
设 ,
,


连接 ,由相切条件知:
,由相切条件知:


同理可求
所以 为定值.
为定值.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,其中
,其中 ,若动直线
,若动直线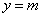 与函数
与函数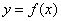 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,则
,则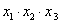 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________. 的左、右焦点分别为F1,F2,线段F1F2被抛物线
的左、右焦点分别为F1,F2,线段F1F2被抛物线 的焦点分成5:3两段,则此双曲线的离心率为______.
的焦点分成5:3两段,则此双曲线的离心率为______. 个项目的比赛安排在
个项目的比赛安排在 个不同的体育馆举办,每个项目的比赛只能安排在一个体育馆进行,则在同一个体育馆比赛的项目不超过
个不同的体育馆举办,每个项目的比赛只能安排在一个体育馆进行,则在同一个体育馆比赛的项目不超过 个的安排方案共有
个的安排方案共有 种 B.
种 B. 种 C.
种 C. 种 D.
种 D. 种
种 的正三角形硬纸,沿各边中点连线垂直折
的正三角形硬纸,沿各边中点连线垂直折 的鸡蛋(视为
的鸡蛋(视为 ”是“
”是“ ”的
”的  ,则
,则 的图象
的图象 轴正半轴有公共点
轴正半轴有公共点  )如图所示,则此几何体的体积是( )
)如图所示,则此几何体的体积是( ) B.3
B.3
 .
.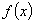 的单调性;
的单调性; 时,证明不等式
时,证明不等式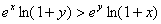 .
.