题目内容
已知△ABC三个顶点的坐标为A(1,3)、B(－1，－1)、C(－3,5)，求这个三角形外接圆的方程．
[解析] 解法一：设圆的方程为(x－a)2＋(y－b)2＝r2，则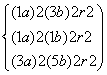
，
整理得
， 解得a＝－2，b＝2，∴r2＝10，
故所求圆的方程为(x＋2)2＋(y－2)2＝10.
解法二：AB的中垂线方程为y－1＝－
(x－0)，BC的中垂线方程为y－2＝
(x＋2)，联立解得圆心坐标为(－2,2)．设圆半径为r，则r2＝(1＋2)2＋(3－2)2＝10，故所求圆的方程为(x＋2)2＋(y－2)2＝10.
解法三：∵kAB＝
＝2，kAC＝
＝－，∴kAB·kAC＝－1，∴AB⊥AC，故△ABC是以A为直角顶点的直角三角形，∴外接圆圆心为BC的中点，即(－2,2)，半径r＝|BC|＝
，所以圆的方程为(x＋2)2＋(y－2)2＝10.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目