题目内容
已知f(x)=sin x+sin .
.
(1)若α∈[0,π],且sin 2α= ,求f(α)的值;
,求f(α)的值;
(2)若x∈[0,π],求f(x)的单调递增区间.
解析 (1)由题设知,f(α)=sin α+cos α.
∵sin 2α= =2sin α·cos α>0,α∈[0,π],
=2sin α·cos α>0,α∈[0,π],
∴α∈ ,sin α+cos α>0.
,sin α+cos α>0.
由(sin α+cos α)2=1+2sin α·cos α= ,
,
得sin α+cos α=
 ,∴f(α)=
,∴f(α)=
 .
.
(2)f(x)= sin
sin ,又0≤x≤π,
,又0≤x≤π,
∴f(x)的单调递增区间为 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =( )
=( ) B.
B. C.-
C.- ,直线
,直线 和
和 是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( )
是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( ) B.
B. C.
C. D.
D.
 是偶函数,则θ的值为________.
是偶函数,则θ的值为________.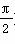 )的最小正周期是π,且f(0)=
)的最小正周期是π,且f(0)=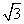 ,则( ).
,则( ).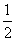 ,φ=
,φ=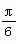 B.ω=
B.ω=
 (ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若x∈
(ω>0)和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若x∈ ,则f(x)的取值范围是________.
,则f(x)的取值范围是________.