题目内容
已知△ABC中,设a,b,c,分别为∠A,∠B,∠C的对边长,AB边上的高与AB边的长相等,则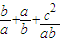 的最大值为 .
的最大值为 .
【答案】分析:由S△ABC= c2=
c2= absinC,
absinC, +
+ +
+ =
= ,再结合余弦定理即可求得答案.
,再结合余弦定理即可求得答案.
解答:解:△ABC中,
∵AB边上的高与AB边的长相等,即S△ABC= c2,
c2,
又S△ABC= absinC,
absinC,
∴c2=absinC,
∴在△ABC中,由余弦定理得:
 +
+ +
+ =
=
=
= -2cosC.
-2cosC.
=2sinC-2cosC
=2 sin(C-
sin(C- )≤2
)≤2 ,当C=
,当C= 时取到等号.
时取到等号.
∴所求关系式的最大值为2 .
.
故答案为:2 .
.
点评:本题考查余弦定理与正弦定理,考查辅助角公式,考查转化与化归思想,属于难题.
 c2=
c2= absinC,
absinC, +
+ +
+ =
= ,再结合余弦定理即可求得答案.
,再结合余弦定理即可求得答案.解答:解:△ABC中,
∵AB边上的高与AB边的长相等,即S△ABC=
 c2,
c2,又S△ABC=
 absinC,
absinC,∴c2=absinC,
∴在△ABC中,由余弦定理得:
 +
+ +
+ =
=
=

=
 -2cosC.
-2cosC.=2sinC-2cosC
=2
 sin(C-
sin(C- )≤2
)≤2 ,当C=
,当C= 时取到等号.
时取到等号.∴所求关系式的最大值为2
 .
.故答案为:2
 .
.点评:本题考查余弦定理与正弦定理,考查辅助角公式,考查转化与化归思想,属于难题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 的最大值为________.
的最大值为________.