题目内容
已知△ABC中，设a，b，c，分别为∠A，∠B，∠C的对边长，AB边上的高与AB边的长相等，则
+
+
的最大值为______．
| b |
| a |
| a |
| b |
| c2 |
| ab |
△ABC中，
∵AB边上的高与AB边的长相等，即S△ABC=
c2，
又S△ABC=
absinC，
∴c2=absinC，
∴在△ABC中，由余弦定理得：
+
+
=
=
=
-2cosC．
=2sinC-2cosC
=2
sin（C-
）≤2
，当C=
时取到等号．
∴所求关系式的最大值为2
．
故答案为：2
．
∵AB边上的高与AB边的长相等，即S△ABC=
| 1 |
| 2 |
又S△ABC=
| 1 |
| 2 |
∴c2=absinC，
∴在△ABC中，由余弦定理得：
| b |
| a |
| a |
| b |
| c2 |
| ab |
| a2+b2+c2 |
| ab |
=
| c2-2abcosC+c2 |
| ab |
=
| 2c2 |
| ab |
=2sinC-2cosC
=2
| 2 |
| π |
| 4 |
| 2 |
| 3π |
| 4 |
∴所求关系式的最大值为2
| 2 |
故答案为：2
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的最大值为________．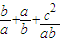
的最大值为 ．