题目内容
椭圆 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|= .
.(I)求椭圆C的方程.
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由.
【答案】分析:(Ⅰ)由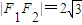 ,知
,知 .由PF1⊥F1F2,知
.由PF1⊥F1F2,知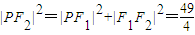 ,
, ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(Ⅱ)设能构成等腰直角三角形ABC,其中B(0,1),由题意可知,直角边BA,BC不可能垂直或平行于x轴,故可设BA边所在直线的方程为y=kx+1(不妨设k<0),则BC边所在直线的方程为y=- ,由
,由 ,得A
,得A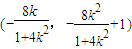 ,
,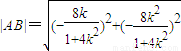 =
=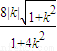 ,由此知存在三个内接等腰直角三角形.
,由此知存在三个内接等腰直角三角形.
解答:解:(Ⅰ)∵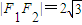 ∴
∴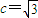
又PF1⊥F1F2,∴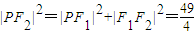 ,
, ,
,
∴2a=|PF1|+|PF2|=4则c=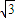 ,∴a=2,b2=1
,∴a=2,b2=1
∴所求椭圆方程为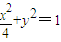 .(6分)
.(6分)
(Ⅱ)设能构成等腰直角三角形ABC,其中B(0,1),
由题意可知,直角边BA,BC不可能垂直或平行于x轴,
故可设BA边所在直线的方程为y=kx+1(不妨设k<0),则BC边所在直线的方程为y=-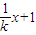 ,
,
由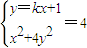 ,得A
,得A ,
,
∴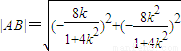 =
=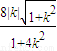 ,(9分)
,(9分)
用-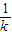 代替上式中的k,得|BC|=
代替上式中的k,得|BC|=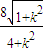 ,由|AB|=|BC|,得|k|(4+k2)=1+4k2
,由|AB|=|BC|,得|k|(4+k2)=1+4k2
∵k<0,∴解得:k=-1或k= ,故存在三个内接等腰直角三角形.(12分)
,故存在三个内接等腰直角三角形.(12分)
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意椭圆性质的灵活运用,合理地进行等价转化.
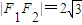 ,知
,知 .由PF1⊥F1F2,知
.由PF1⊥F1F2,知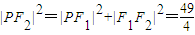 ,
, ,由此能求出椭圆方程.
,由此能求出椭圆方程.(Ⅱ)设能构成等腰直角三角形ABC,其中B(0,1),由题意可知,直角边BA,BC不可能垂直或平行于x轴,故可设BA边所在直线的方程为y=kx+1(不妨设k<0),则BC边所在直线的方程为y=-
 ,由
,由 ,得A
,得A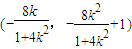 ,
,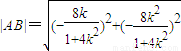 =
=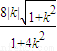 ,由此知存在三个内接等腰直角三角形.
,由此知存在三个内接等腰直角三角形.解答:解:(Ⅰ)∵
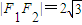 ∴
∴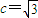
又PF1⊥F1F2,∴
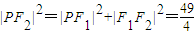 ,
, ,
,∴2a=|PF1|+|PF2|=4则c=
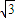 ,∴a=2,b2=1
,∴a=2,b2=1∴所求椭圆方程为
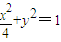 .(6分)
.(6分)(Ⅱ)设能构成等腰直角三角形ABC,其中B(0,1),
由题意可知,直角边BA,BC不可能垂直或平行于x轴,
故可设BA边所在直线的方程为y=kx+1(不妨设k<0),则BC边所在直线的方程为y=-
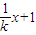 ,
,由
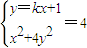 ,得A
,得A ,
,∴
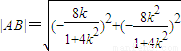 =
=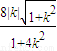 ,(9分)
,(9分)用-
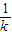 代替上式中的k,得|BC|=
代替上式中的k,得|BC|=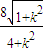 ,由|AB|=|BC|,得|k|(4+k2)=1+4k2
,由|AB|=|BC|,得|k|(4+k2)=1+4k2∵k<0,∴解得:k=-1或k=
 ,故存在三个内接等腰直角三角形.(12分)
,故存在三个内接等腰直角三角形.(12分)点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意椭圆性质的灵活运用,合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目