题目内容
7．若A（2，-1），B（4，3）到直线l的距离相等，且l过点P（1，1），则直线1的方程为（ ）| A． | 2x-y-1=0 | B． | x-2y+1=0 | C． | x=1或x-2y+1=0 | D． | y=1或2x-y-1=0 |
分析 由题意可得直线l与AB平行或直线l经过线段AB的中点，分类讨论，用待定系数法求直线l的方程．
解答 解：若直线1和直线AB平行，由于KAB=$\frac{3+1}{4-2}$=2，则由l过点P（1，1），
可得直线1的方程为y-1=2（x-1），即 2x-y-1=0．
若直线1经过线段AB的中点（3，1），则由l过点P（1，1），
故直线l的方程为y=1．
综上可得，直线l的方程为2x-y-1=0或y=1，
故选：D．
点评 本题主要考查用待定系数法求直线的方程，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．已知函数f（x）=|2x-1|，g（x）=x2-（2+3k）x+2k+1，若函数y=g[f（x）]有3个不同零点，则k的范围是（ ）
| A． | k=-$\frac{1}{2}$或k＞0 | B． | -$\frac{1}{2}$＜k＜0或k＞0 | C． | k≥-$\frac{1}{2}$ | D． | k≥0 |
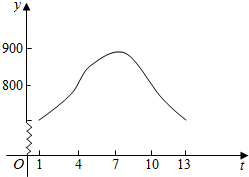某地昆虫种群数量在七月份1～13日的变化如图所示，且满足y=Asin（ωx+φ）（ω＞0，φ＜0）．