题目内容
设数列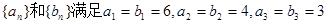 ,且数列
,且数列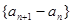 是等差数列,
是等差数列,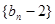 是等比数列.
是等比数列.
(1)求数列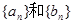 的通项公式;
的通项公式;
(2)设数列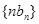 的前
的前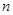 项和为
项和为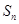 ,求
,求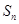 的表达式;
的表达式;
(3)数列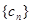 满足
满足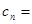
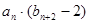 ,求数列
,求数列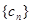 的最大项.
的最大项.
(1)


(2)
(3)数列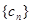 是单调递减数列,最大项是
是单调递减数列,最大项是
解析试题分析:解:(1)依题意得:(
所以 2分
2分
故当 时,有
时,有

 , 3分
, 3分
又因为n=1时, 也适合上式,
也适合上式,
所以
 4分
4分
又


故 6分
6分
(2)


 7分
7分
令
则 8分
8分
上面两式相减得,
那么

所以 10分
10分
(3)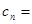

令 , 12分
, 12分
得
而 显然对任意的正整数
显然对任意的正整数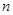 都成立,
都成立,
所以数列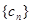 是单调递减数列,最大项是
是单调递减数列,最大项是 . 14分
. 14分
考点:等比数列,累加法
点评:主要是通过递推关系式采用累加法求解通项公式和结合等比数列的公式求解,同时结合函数的性质来判定数列的单调性,进而求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的公差为
的公差为 ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前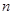 项和
项和 .
.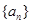 的前
的前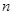 项和
项和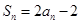 .数列
.数列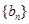 满足:
满足: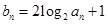 .
.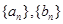 的通项
的通项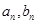 .并比较
.并比较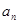 与
与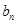 的大小;
的大小;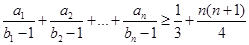 .
.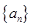 的前
的前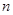 项和
项和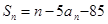 ,
,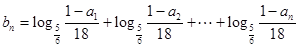 ,求数列
,求数列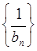 的前
的前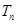 .
.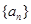 的前
的前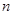 项和为
项和为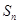 ,
,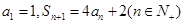 .
.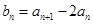 ,求
,求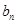 ;
;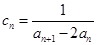 ,求
,求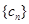 的前6项和
的前6项和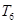 .
.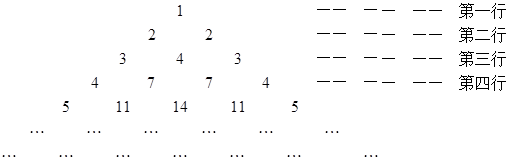
 行的第二个数为
行的第二个数为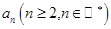
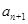 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出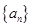 的通项公式
的通项公式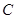 :
: ,数列
,数列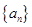 的首项
的首项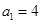 ,且
,且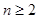 时,点
时,点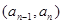 恒在曲线
恒在曲线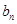 }满足
}满足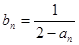
 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;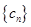 满足
满足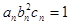 ,试比较数列
,试比较数列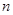 项和
项和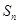 与
与 的大小.
的大小.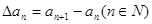 。
。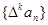 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。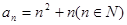 ,试判断
,试判断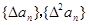 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?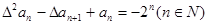 ,求数列{an}的通项公式。
,求数列{an}的通项公式。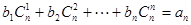 对一切自然
对一切自然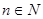 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。