题目内容
数列{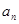 }中,a1=3,
}中,a1=3,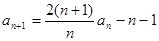 ,
,
(1)求a1、a2、a3、a4;
(2)用合情推理猜测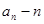 关于n的表达式(不用证明);
关于n的表达式(不用证明);
(3)用合情推理猜测{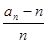 }是什么类型的数列并证明;
}是什么类型的数列并证明;
(4)求{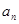 }的前n项的和。
}的前n项的和。
(1)3,10,27,68
(2) an-n=n 2n
2n
(3) =2
=2 2n-1,
2n-1,
解析试题分析:解:(1) a1=3, a2= a1-1-1=10,a3=
a1-1-1=10,a3= a2-2-1=27,
a2-2-1=27,
a4=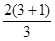 a3-3-1=68 2分
a3-3-1=68 2分
(2)由(1),a1-1=2=1 2,a2-2=8=2
2,a2-2=8=2 22,a3-3=24=3
22,a3-3=24=3 23,a4-4=64=4
23,a4-4=64=4 24,
24,
猜测an-n=n 2n, 4分
2n, 4分
(3) 由(2),an-n=n 2n,
2n, =
= 2n,因此可推测{
2n,因此可推测{ }是等比数列 5分证明如下:
}是等比数列 5分证明如下: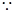 an+1=
an+1= an-n-1,
an-n-1, an+1-(n+1)=
an+1-(n+1)=  an-2(n+1)=2(n+1)(
an-2(n+1)=2(n+1)( -1),
-1),
 =2
=2
 , 而
, 而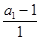 =2
=2 0,
0,  {
{ }是首项为2,公比为2的等比
}是首项为2,公比为2的等比
数列; 8分
(4)由(3) =2
=2 2n-1,
2n-1, an="n+" n 2n, 10分
an="n+" n 2n, 10分
{an}的前n项的和: Sn= +1
+1 2+2
2+2 22+3
22+3 23+ +n
23+ +n 2n。
2n。
记P=1 2+2
2+2 22+3
22+3 23+ +n
23+ +n 2n,则2P-P= n
2n,则2P-P= n 2n+1-(2+22+23+ +2n)= (n-1)
2n+1-(2+22+23+ +2n)= (n-1) 2n+1+2
2n+1+2 P=(n-1)
P=(n-1) 2n+1+2,
2n+1+2,  Sn=
Sn= +(n-1)
+(n-1) 2n+1+2. 13分
2n+1+2. 13分
考点:合情推理
点评:解决的关键是能根据递推关系来归纳猜想来得到数列的通项公式的特点,进而分析证明,属于基础题。

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
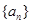 的前
的前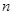 项和
项和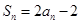 .数列
.数列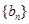 满足:
满足: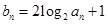 .
.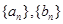 的通项
的通项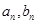 .并比较
.并比较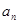 与
与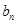 的大小;
的大小;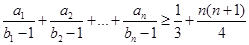 .
.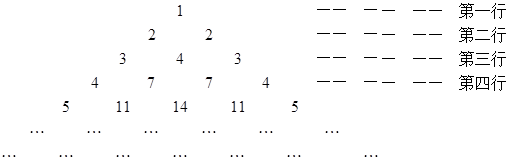
 行的第二个数为
行的第二个数为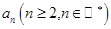
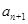 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出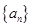 的通项公式
的通项公式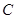 :
: ,数列
,数列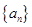 的首项
的首项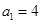 ,且
,且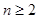 时,点
时,点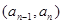 恒在曲线
恒在曲线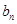 }满足
}满足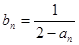
 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;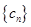 满足
满足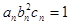 ,试比较数列
,试比较数列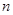 项和
项和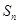 与
与 的大小.
的大小.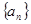 中,
中,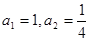 ,且
,且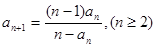 .
.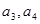 ,猜想
,猜想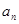 的表达式,并加以证明;
的表达式,并加以证明;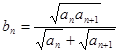 ,求证:对任意的自然数
,求证:对任意的自然数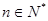 都有
都有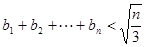 .
. 的前
的前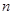 项和记为
项和记为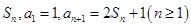
 的各项为正,其前
的各项为正,其前 ,且
,且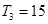 ,又
,又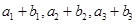 成等比数列,求
成等比数列,求 的通项公式为
的通项公式为
 的值;
的值; 的值,并用数学归纳法证明你的猜想.
的值,并用数学归纳法证明你的猜想.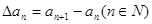 。
。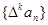 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。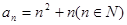 ,试判断
,试判断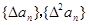 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?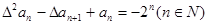 ,求数列{an}的通项公式。
,求数列{an}的通项公式。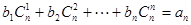 对一切自然
对一切自然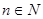 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。