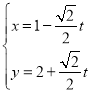题目内容
【题目】如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]()
![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点,![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 的面积最大值为1.
的面积最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,过点![]() 作两条直线与椭圆
作两条直线与椭圆![]() 分别交于
分别交于![]() ,且使
,且使![]() 轴,问四边形
轴,问四边形![]() 的两条对角线的交点是否为定点?若是,求出该定点的坐标;若不是,请说明理由.
的两条对角线的交点是否为定点?若是,求出该定点的坐标;若不是,请说明理由.

【答案】(1)![]() (2)定点坐标为
(2)定点坐标为![]() .
.
【解析】分析:(Ⅰ)![]() 意味着通径的一半
意味着通径的一半![]() ,
,![]() 最大面积为
最大面积为![]() ,所以
,所以![]() ,故椭圆的方程为
,故椭圆的方程为![]() .
.
(Ⅱ)根据对称性,猜测定点必定在![]() 轴上,故可设
轴上,故可设![]() ,
,![]() ,则
,则![]() ,
,![]() ,再设
,再设![]() ,根据
,根据![]() 三点共线可以得到
三点共线可以得到![]() ,联立直线
,联立直线![]() 和椭圆的标准方程后消去
和椭圆的标准方程后消去![]() ,利用韦达定理可以得到
,利用韦达定理可以得到![]() ,从而
,从而![]() 过定点
过定点![]() ,同理直线
,同理直线![]() 也过
也过![]() 即两条直线交于定点
即两条直线交于定点![]() .
.
详解:(Ⅰ)设![]() ,由题意可得
,由题意可得![]() ,即
,即![]() .
.
∵![]() 是
是![]() 的中位线,且
的中位线,且![]() ,
,
∴![]() ,即
,即![]() ,整理得
,整理得![]() .①
.①
又由题知,当![]() 在椭圆
在椭圆![]() 的上顶点时,
的上顶点时,![]() 的面积最大,
的面积最大,
∴![]() ,整理得
,整理得![]() ,即
,即![]() ,②
,②
联立①②可得![]() ,变形得
,变形得![]() ,解得
,解得![]() ,进而
,进而![]() .
.
∴椭圆![]() 的方程式为
的方程式为![]() .
.
(Ⅱ)设![]() ,
,![]() ,则由对称性可知
,则由对称性可知![]() ,
,![]() .
.
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立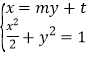 ,消去
,消去![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
由![]() 三点共线
三点共线![]() ,即
,即![]() ,
,
将![]() ,
,![]() 代入整理得
代入整理得![]() ,
,
即![]() ,从而
,从而![]() ,化简得
,化简得![]() ,解得
,解得![]() ,于是直线
,于是直线![]() 的方程为
的方程为![]() , 故直线
, 故直线![]() 过定点
过定点![]() .同理可得
.同理可得![]() 过定点
过定点![]() ,
,
∴直线![]() 与
与![]() 的交点是定点,定点坐标为
的交点是定点,定点坐标为![]() .
.

【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
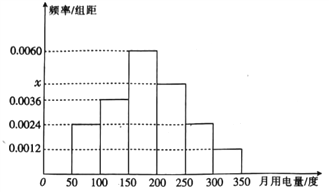
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
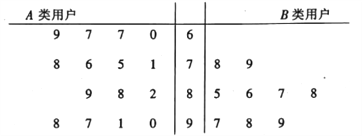
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
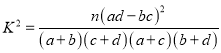 ,
, ![]() .
.