题目内容
1.已知抛物线y2=4x的焦点为F,其准线与x轴的交点为K,P为抛物线上的点,设|PK|=t|PF|,则实数t的取值范围是[1,$\sqrt{2}$].分析 由题意可得F(1,0),K(-1,0),过点P作PH垂直于准线x=-1,垂足为H,由条件可得t=$\frac{|PK|}{|PF|}$=$\frac{|PK|}{|PH|}$,当点P与原点O重合时,|PH|=|PK|,t有最小值为1;当直线MN和抛物线相切时,t=$\frac{|PK|}{|PF|}$=$\frac{|PK|}{|PH|}$=$\frac{1}{cosθ}$有最大值.求出切线的斜率,即可求出的t最大值.
解答 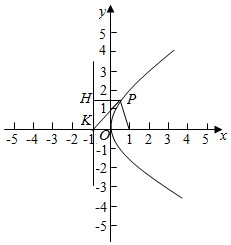 解:由题意可得F(1,0),K(-1,0),过点P作PH垂直于准线x=-1,垂足为H,
解:由题意可得F(1,0),K(-1,0),过点P作PH垂直于准线x=-1,垂足为H,
由抛物线的定义可得|PF|=|PH|
由条件可得t=$\frac{|PK|}{|PF|}$=$\frac{|PK|}{|PH|}$
如图所示:
故当点P与原点O重合时,|PH|=|PK|,t有最小值为1.
当直线PK和抛物线相切时,t=$\frac{|PK|}{|PF|}$=$\frac{|PK|}{|PH|}$=$\frac{1}{cosθ}$有最大值,这里θ=∠PKF.
设当直线PK和抛物线相切时,PK的方程为x=my-1,代入抛物线方程化简可得y2-4my+4=0.
由题意可得,此方程的判别式△=0,即16m2-16=0,∴m=±1,即 tanθ=1,
故cosθ=$\frac{\sqrt{2}}{2}$,故t的最大值为$\sqrt{2}$.
综上可得t∈[1,$\sqrt{2}$],
故答案为:[1,$\sqrt{2}$].
点评 本题主要考查抛物线的定义、标准方程,以及简单性质的应用,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
11.已知实数a,b满足关系a2=b2-b+1,则下列结论正确的是( )
| A. | 若a<1,b<$\frac{1}{2}$,则a>b | B. | 若a<1,b<$\frac{1}{2}$,则a<b | ||
| C. | 若a>1,b>$\frac{1}{2}$,则a>b | D. | 若a>1,b>$\frac{1}{2}$,则a<b |
12.已知全集U=R,集合A={x|y=log2(x-1)},B={y|y=2x},则B∩(∁UA)为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,2) |
6.设全集为R,集合A={x|$\frac{1-x}{1+x}$≥0},B={x|-2≤x<0},则(∁RA)∩B=( )
| A. | (-1,0) | B. | [-1,0) | C. | [-2,-1] | D. | [-2,-1) |
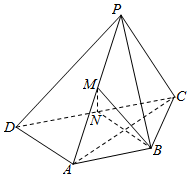 如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.