题目内容
已知函数 ,
, 且
且 ).
).
(1)讨论函数 的单调性;
的单调性;
(2)若 ,方程
,方程 有惟一解时,求
有惟一解时,求 的值。
的值。
(1) 当 是偶数时,
是偶数时,  在
在 上是增函数;当
上是增函数;当 是奇数时
是奇数时 在
在 是减函数,在
是减函数,在 是增函数;(2)
是增函数;(2) .
.
【解析】
试题分析:(1)求单调区间,弦确定定义域,利用求导得: ,再按k是偶数时,
,再按k是偶数时, 和k是奇数时,进行分情况,分别求得导函数大于零和小于零,进而求得单调区间;(2)当
和k是奇数时,进行分情况,分别求得导函数大于零和小于零,进而求得单调区间;(2)当 时,方程
时,方程 有唯一解,令
有唯一解,令 ,利用求导进一步得,
,利用求导进一步得, 在
在 单调递减,在
单调递减,在 单调递增,所以要满足题意,只需使
单调递增,所以要满足题意,只需使 有唯一解,只需使
有唯一解,只需使 ,进而求得
,进而求得 的值.
的值.
试题解析:(1)由已知得, 且
且 .
.
当 是偶数时,则
是偶数时,则 ,则
,则 在
在 上是增函数; (2分)
上是增函数; (2分)
当 是奇数时,则,
是奇数时,则, , (3分)
, (3分)
所以当x
 时,
时, , 当x
, 当x
 时,
时, ,
,
故当 是偶数时,
是偶数时,  在
在 上是增函数;
上是增函数;
当 是奇数时
是奇数时 在
在 是减函数,在
是减函数,在 是增函数. (5分)
是增函数. (5分)
(Ⅱ)若 ,则
,则 )
)
记 ,
,  ,
,
若方程 有唯一解,即
有唯一解,即 有唯一解; (6分)
有唯一解; (6分)
令 ,得
,得 ,
,
 (舍去)
(舍去) (7分)
(7分)
当 时,
时, ,
, 在
在 是单调递减函数;
是单调递减函数;
当 时,
时, ,
, 在
在 上是单调递增函数。
上是单调递增函数。
当 时,
时,  ,
, (8分)
(8分)
 有唯一解,
有唯一解,
则 ,即
,即 (9分)
(9分)
 (10分)
(10分)
设函数 ,
,
∵在 时,
时, 是增函数,
是增函数, 至多有一解。
至多有一解。
 , ∴方程(*)的解为
, ∴方程(*)的解为 ,即
,即 ,解得
,解得 。 (12分)
。 (12分)
考点:1.利用导函数求函数的单调性;2.分类讨论思想;3.零点的个数问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,则
,则

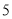 和
和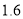 (B)
(B)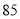 和
和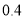 (D)
(D)  图象的是
图象的是
 ,若
,若 ,则
,则 等于
等于 满足
满足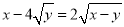 ,则
,则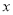 的取值范围是____________________.
的取值范围是____________________. 是椭圆
是椭圆 的两焦点,过点
的两焦点,过点 的直线交椭圆于点
的直线交椭圆于点 ,若
,若 ,则
,则 ( )
( ) :
: ,
, 的一边
的一边 为圆
为圆 长度的最大值是 .
长度的最大值是 .