题目内容
13.设数列{an}的前n项和为Sn,满足a1=1,2Sn=an+1-1.(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=log3an+1,数列{bn}的前n项和为Tn,求数列{$\frac{1}{{T}_{n}}$}的前n项和.
分析 (Ⅰ)由条件,将n换为n-1,两式相减,求出a2=3,再由等比数列的通项公式,即可得到所求;
(Ⅱ)bn=log3an+1=log33n=n,运用等差数列的求和公式可得Tn,再由$\frac{1}{{T}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),运用裂项相消求和,化简即可得到所求和.
解答 解:(Ⅰ)a1=1,2Sn=an+1-1,
可得2Sn-1=an-1,(n≥2),
两式相减可得,2an=2Sn-2Sn-1=an+1-an,
即有an+1=3an(n≥2),
由2a1=2S1=a2-1,可得a2=3,
则an=a2qn-2=3•3n-2=3n-1,对n=1也成立,
则{an}的通项公式为an=3n-1;
(Ⅱ)bn=log3an+1=log33n=n,
则前n项和为Tn=$\frac{1}{2}$n(n+1),
可得$\frac{1}{{T}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
则数列{$\frac{1}{{T}_{n}}$}的前n项和为2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
点评 本题考查数列的通项公式的求法,注意运用数列递推式,考查数列的求和方法:直接法和裂项相消求和,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
1.已知圆C1:x2+y2+4x-4y-3=0,动点P在圆C2:x2+y2-4x-12=0上,则△PC1C2面积的最大值为( )
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 8$\sqrt{5}$ | D. | 20 |
8.已知O为坐标原点,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,双曲线C上一点P满足PF1⊥PF2,且|PF1||PF2|=2a2,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
7.下列函数中,在区间(0,+∞)上单调递增且为偶函数的是( )
| A. | y=x3 | B. | y=2x | ||
| C. | y=[x](不超过x的最大整数) | D. | y=|x| |
4.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若|PF1|=1,则|PF2|=( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
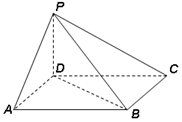 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.