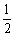题目内容
如图(6),已知 是椭圆
是椭圆 的右焦点;
的右焦点;

 与
与 轴交于
轴交于 两点,其中
两点,其中 是椭圆
是椭圆 的左焦点.
的左焦点.
(1)求椭圆 的离心率;
的离心率;
(2)设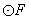 与y轴的正半轴的交点为
与y轴的正半轴的交点为 ,点
,点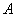 是点
是点 关于y轴的对称点,
关于y轴的对称点,
试判断直线 与
与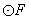 的位置关系;
的位置关系;
(3)设直线 与椭圆
与椭圆 交于另一点
交于另一点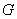 ,若
,若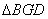 的面积为
的面积为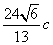 ,求椭圆
,求椭圆 的标准方程.
的标准方程.

解:(1)∵圆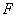 过椭圆
过椭圆 的左焦点,把
的左焦点,把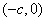 代入圆
代入圆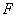 的方程,得
的方程,得
 ,故椭圆
,故椭圆 的离心率
的离心率 ;
;
(2) 在方程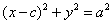 中令
中令 得
得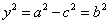 ,可知点
,可知点 为椭圆的上顶点,
为椭圆的上顶点,
由(1)知,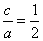 ,故
,故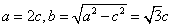 ,故
,故
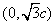 ,
,
在圆F的方程中令y=0可得点D坐标为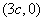 ,则点A为
,则点A为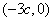 ,
,
于是可得直线AB的斜率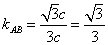 ,
,
而直线FB的斜率 ,
,
∵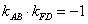 ,
,
∴直线AB与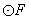 相切。
相切。
(3)椭圆的方程可化为
由(2)知切线 的方程为
的方程为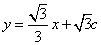 -
-
解方程组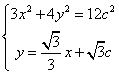 ,得点
,得点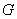 的坐标为
的坐标为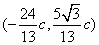
而点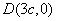 到直线
到直线 的距离
的距离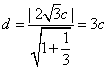 ,
,
由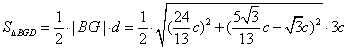
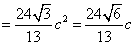
解得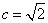 ,
,
∴椭圆的标准方程为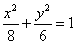 .
.

练习册系列答案
相关题目
 ,其中
,其中
 是自然对数的底数.
是自然对数的底数. 的零点;
的零点;
 均有两个极值点,一个在区间
均有两个极值点,一个在区间 内,另一个在区间
内,另一个在区间 外,
外, 的取值范围;
的取值范围; 且函数
且函数 在
在 上是单调函数,探究函数
上是单调函数,探究函数 的单调性.
的单调性.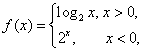 则
则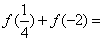 ______.
______.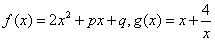 是定义在集合
是定义在集合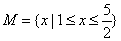 上的两个函数.对任意的
上的两个函数.对任意的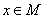 ,存在常数
,存在常数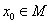 ,使得
,使得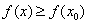 ,
,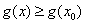 ,且
,且 .则函数
.则函数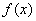 在集合
在集合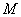 上的最大值为
上的最大值为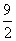 B.4 C. 6 D.
B.4 C. 6 D. 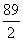
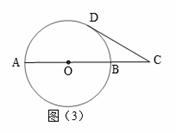
 ,运算原理如上图所示,则式子
,运算原理如上图所示,则式子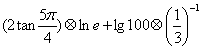 的值为( )
的值为( )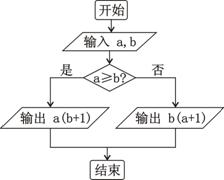
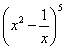 的展开式中,含
的展开式中,含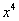 的项的系数是 .
的项的系数是 .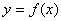
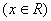 满足
满足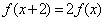 ,且
,且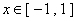 时,
时,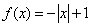 ,则当
,则当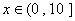 时,
时, 的图象的交点个数为( )
的图象的交点个数为( )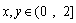 且
且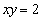 ,使不等式
,使不等式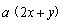 ≥
≥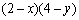 恒成立,则实数
恒成立,则实数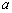 的取值范围为( )
的取值范围为( )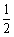 B.
B.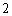 C.
C.