题目内容
已知函数 ,其中
,其中
 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意
 均有两个极值点,一个在区间
均有两个极值点,一个在区间 内,另一个在区间
内,另一个在区间 外,
外,
求 的取值范围;
的取值范围;
(3)已知 且函数
且函数 在
在 上是单调函数,探究函数
上是单调函数,探究函数 的单调性.
的单调性.
解:(1) ,
,

① 当 时,
时, 函数
函数 有1个零点:
有1个零点: ② 当
② 当 时,
时, 函数
函数 有2个零点:
有2个零点: ③ 当
③ 当 时,
时, 函数
函数 有两个零点:
有两个零点:
④ 当 时,
时, 函数
函数 有三个零点:
有三个零点:

(2)
设 ,
, 的图像是开口向下的抛物线.
的图像是开口向下的抛物线.
由题意对任意
 有两个不等实数根
有两个不等实数根 ,
,
且
则对任意
 ,即
,即 ,
,
又任意
 关于
关于 递增,
递增, ,
,
故
所以 的取值范围是
的取值范围是
(3)由(2)知, 存在
 ,又函数
,又函数 在
在 上是单调函数,故函数
上是单调函数,故函数 在
在 上是单调减函数,
上是单调减函数,
从而 即
即
所以
由 知
知
即对任意

故函数 在
在 上是减函数.
上是减函数.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 是
是 有实根的( )
有实根的( ) 的单调减区间是 .为 .
的单调减区间是 .为 . ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为
,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为 的样本,则应从高二年级抽取 名学生.
的样本,则应从高二年级抽取 名学生. 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为

 ,
, .
. ;
; 求
求 的值.
的值.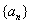 中,若
中,若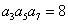 ,则
,则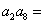 ( )
( )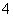 B .
B .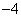 C .
C .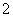 D.-2
D.-2 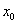 附近的左侧
附近的左侧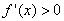 ,右侧
,右侧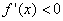 ,那么
,那么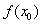 是极大值.
是极大值.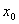 附近的左侧
附近的左侧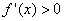 ,右侧
,右侧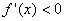 ,那么
,那么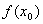 是极小值.
是极小值.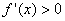 ,那么
,那么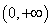 上单调递减的函数是( )
上单调递减的函数是( )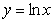 B.
B.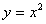 C.
C.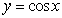 D.
D.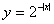
 是椭圆
是椭圆 的右焦点;
的右焦点;
 与
与 轴交于
轴交于 两点,其中
两点,其中 是椭圆
是椭圆 的左焦点.
的左焦点.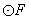 与y轴的正半轴的交点为
与y轴的正半轴的交点为 ,点
,点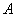 是点
是点 关于y轴的对称点,
关于y轴的对称点, 与
与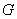 ,若
,若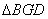 的面积为
的面积为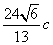 ,求椭圆
,求椭圆