题目内容
18.A,B两地相距300km,汽车从A地以vkm/h的速度匀速行驶到B地(速度不得超过60km/h).已知汽车每小时的运输成本由固定成本和可变成本组成,固定成本为250元,可变成本(单位:元)与速度v的立方成正比,比例系数$\frac{1}{1000}$,设全程的运输成本为y元.(1)求y关于v的函数关系;
(2)为使全程运输成本最小,汽车应以多大速度行驶?
分析 (1)求出汽车从A地匀速行驶到B地所用时间,根据汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可得全程运输成本,及函数的定义域;
(2)利用基本不等式可得结论.
解答 解:(1)依题意知汽车从A地匀速行驶到B地所用时间为$\frac{300}{v}$,
全程运输成本为y=$\frac{300}{v}$(250+$\frac{1}{1000}{v}^{3}$),即y=300($\frac{250}{v}$+$\frac{1}{1000}{v}^{2}$),定义域为(0,60],
(2)y=300($\frac{250}{v}$+$\frac{1}{1000}{v}^{2}$)=300($\frac{125}{v}$+$\frac{125}{v}$+$\frac{1}{1000}{v}^{2}$)≥300×3$\root{3}{\frac{125×125}{1000}}$=2250,
当且仅当$\frac{125}{v}$=$\frac{1}{1000}{v}^{2}$,即v=50km/h时,全程运输成本最小,最小为2250元.
点评 本题考查函数模型的构建,考查基本不等式的运用,解题的关键是构建函数模型,利用基本不等式求最值.

练习册系列答案
相关题目
8.已知函数f(x)=ax3+x+1的图象在点(1,f(1))的处的切线过点(2,11),则 a=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2 |
6.判断:“如果一个事件是随机事件,则它发生的概率P的取值范围是(0,1)”的真假是( )
| A. | 假命题 | B. | 真命题 | C. | 不是命题 | D. | 可真可假 |
8.方程3x+4x=5x解的情况是( )
| A. | 有且只有一个根2 | B. | 不仅有根2还有其他根 | ||
| C. | 有根2和另一个负根 | D. | 有根2和另一个正根 |
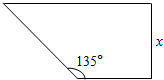 某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).
某植物园要建形状为直角梯形的苗圃(如图所示),两条邻边借用夹角为135°的两面墙,另两条边的总长为60m,设垂直于底边的腰长为x(m).