题目内容
在 △ABC 中,角 A, B, C 所对的边分别为a ,b ,c , 且 C =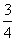 π ,s i nA =
π ,s i nA =  ,c - a = 5 - 10 , 则b = .
,c - a = 5 - 10 , 则b = .
5

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
题目内容
在 △ABC 中,角 A, B, C 所对的边分别为a ,b ,c , 且 C =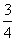 π ,s i nA =
π ,s i nA =  ,c - a = 5 - 10 , 则b = .
,c - a = 5 - 10 , 则b = .
5

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案