题目内容
4．函数f（x）=$\frac{1}{12}$x4-$\frac{1}{2}$ax2，若f（x）的导函数f′（x）在R上是增函数，求实数a的取值范围是？分析 由求导公式和法则求出f′（x）和f″（x），由条件和导数与函数单调性的关系列出不等式后，由恒成立问题求出函数的最值，可得a的取值范围．
解答 解：由题意得，f′（x）=$\frac{1}{3}{x}^{3}-ax$，
因为导函数f′（x）在R上是增函数，
所以f″（x）=x2-a≥0在R上恒成立，
则a≤x2，即a≤0，
所以数a的取值范围是（-∞，0]．
点评 本题考查求导公式和法则，导数与函数单调性的关系，以及恒成立问题的转化，属于中档题．
练习册系列答案
相关题目
15．已知全集U=R，集合A={x|x+1＜0}，B={x|x2+3x＜0}，则 A∩B等于（ ）
| A． | {x|-3＜x＜0} | B． | {x|-3＜x＜-1} | C． | {x|x＜-1} | D． | {x|-1≤x＜0} |
19．下列命题中不正确的是（ ）
| A． | logab•logbc•logca=1（a，b，c均为不等于1的正数） | |
| B． | 若xlog34=1，则${4^x}+{4^{-x}}=\frac{10}{3}$ | |
| C． | 函数f（x）=lnx满足f（a+b）=f（a）•f（b）（a，b＞0） | |
| D． | 函数f（x）=lnx满足f（a•b）=f（a）+f（b）（a，b＞0） |
9．已知函数f（x）=ex+elnx-2ax在x∈（1，3）上单调递增，则实数a的取值范围为（ ）
| A． | （-∞，$\frac{{e}^{3}}{2}$+$\frac{e}{6}$） | B． | [（$\frac{{e}^{3}}{2}$+$\frac{e}{6}$，+∞） | C． | （-∞，e） | D． | （-∞，e） |
13．函数y=xsinx的部分图象是（ ）
| A． |  | B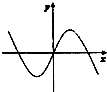． |  | C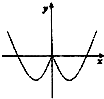． |  | D． |  |
