Question

14．已知函数f（x）=x²-2（a+2）x+a²，g（x）=-x²+2（a-2）x-a²+8．设H₁（x）=max{f（x），g（x）}，H₂（x）=min{f（x），g（x）}，若max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值．记H₁（x）的最小值为A，H₂（x）的最大值为B，则B-A=16．

Answer 1

分析 本选择题宜采用特殊值法．取a=-2，则f（x）=x²+4，g（x）=-x²-8x+4．画出它们的图象，如图所示．从而得出H₁（x）的最小值为两图象右边交点的纵坐标，H₂（x）的最大值为两图象左边交点的纵坐标，再将两函数图象对应的方程组成方程组，求解即得．

解答 解：取a=-2，则f（x）=x²+4，g（x）=-x²-8x+4．画出它们的图象，如图所示．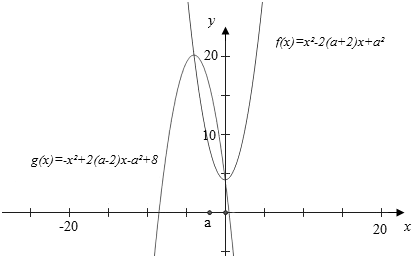

则H₁（x）的最小值为两图象右边交点的纵坐标，H₂（x）的最大值为两图象左边交点的纵坐标，
由$\left\{\begin{array}{l}{y={x}^{2}+4}\\{y=-{x}^{2}-8x+4}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=20}\end{array}\right.$，
∴A=4，B=20，B-A=16．
故答案为：16．

点评 本题主要考查了二次函数的图象与性质、函数最值的应用等，考查了数形结合的思想，属于中档题．