题目内容

记向量
OA
=
a
，
OB
=
b
，其中O为直角坐标原点，且
a
=（3，1），
b
=（1，3），向量
OC
=λ
a
+μ
b
，且0≤λ≤μ≤1，则点C点所有可能的位置区域的面积为
 
．
考点：简单线性规划
专题：不等式的解法及应用
分析：由
a
=（3，1），
b
=（1，3），向量
OC
=λ
a
+μ
b
，知 
OC
=（3λ，λ）+（μ，3μ）=（3λ+μ，λ+3μ），由0≤λ≤μ≤1，然后推出约束条件，由此能求解三角形的面积．
解答： 解：设
OC
=（x，y）=（3λ+μ，λ+3μ）
∴
x=3λ+μ
y=λ+3μ
∴
3y-x=8μ
3x-y=8λ

由已知0≤8λ≤8μ≤8，得0≤3x-y≤3y-x≤8，
得
3x-y≥0
y≥x
3y-x≤8
 区域如图阴影部分，
得三角形顶点B（1，3），C（4，4），|OC|=4
2
，
点B到直线x-y=0距离d=
2
2
=
2
，
故S=
1
2
×4
2
×
2
=4．
故答案为：4．
点评：本题考查平面向量的综合题，线性规划的应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
在平面直角坐标系xOy中，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1（-c，0），F2（c，0），已知点（1，e）和（e，
3
2
）都在椭圆C上，其中e为椭圆C的离心率．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线l：y=kx+m与椭圆C相交于P，Q两点，若在椭圆C上存在点R，使四边形OPRQ为平行四边形，求m的取值范围．
在数列{an}中，a1=3，点列（
an
，
an-1
）（其中n∈N*，且n＞1）在直线x-y-
3
=0上，则数列{an}的通项公式an=
 
．
以平面直角坐标系的原点为极点，以x轴的正半轴为极轴，建立极坐标系，则圆x2+y2=2上的点到曲线ρcosθ+ρsinθ=4（ρ，θ∈R）的最短距离是
 
．
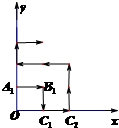某地区为了绿化环境进行大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在点A1（0，1），第二棵树在点B1（1，1），第三棵树在点C1（1，0），第四棵树在点C2（2，0），接着按图中箭头方向每隔一个单位种一棵树，那么
（1）第n棵树所在点坐标是（3，1），则n=
 
；
（2）第2014棵树所在点的坐标是
 
．
过点M（-3，-
3
2
）且被圆x2+y2=25截得弦长为8的直线的方程为
 
．
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则可求得：f（
1
4
）+f（
2
4
）+f（
3
4
）+f（
4
4
）+f（
5
4
）+f（
6
4
）+f（
7
4
）=
 
．
下列四个命题：
①利用计算机产生0～1之间的均匀随机数a，则事件“3a-1＞0”发生的概率为
1
3
；
②“x+y≠0”是“x≠1或y≠1”的充分不必要条件；
③命题“在△ABC中，若sinA=sinB，则△ABC为等腰三角形”的否命题为真命题；
④2，3，5，7，8，8这组数的极差与中位数相等
其中说法正确的个数是（　　）
A、3个B、2个C、1个D、0个
设复数z=-3i+1，则z的共轭复数在复平面内对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网