题目内容
4.解不等式:3×4x-2×6x>0.分析 把原不等式变形,即$(\frac{2}{3})^{x}>\frac{2}{3}$,然后由指数函数的单调性得答案.
解答 解:由3×4x-2×6x>0,得3×4x>2×6x,
即$(\frac{2}{3})^{x}>\frac{2}{3}$,∴x<1.
∴不等式3×4x-2×6x>0的解集为(-∞,1).
点评 本题考查指数不等式的解法,考查指数函数的单调性,是基础题.

练习册系列答案
相关题目
12.已知a=log3$\frac{1}{4}$,b=3${\;}^{-\frac{1}{3}}$,c=log${\;}_{\frac{1}{2}}$2,则( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
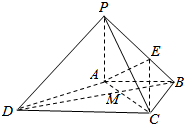 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥DC,AB⊥BC,且PA=AB=BC=$\frac{1}{2}$CD,BE=$\frac{1}{3}$BP.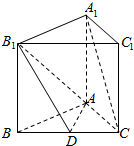 已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.
已知正三棱柱ABC-A1B1C1中,BC=1,D是棱BC上的动点.