题目内容
若点M是△ABC所在平面内的一点,且满足 ,则△ABM与△ABC的面积比为________.
,则△ABM与△ABC的面积比为________.

分析:连接AM,BM,延长AC至D使AD=3AC,延长AM至E使AE=5AM,连接BE,则四边形ABED是平行四边形,利用S△ABC=
 S△ABD
S△ABD,S△AMB=
 S△ABE,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半,即可求得结论.
S△ABE,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半,即可求得结论.解答:M是△ABC所在平面内一点,连接AM,BM,延长AC至D使AD=3AC,延长AM至E使AE=5AM.
∵
 ,
,∴
 ,
,连接BE,则四边形ABED是平行四边形(向量AB和向量DE平行且模相等)
由于
 ,所以S△ABC=
,所以S△ABC= S△ABD
S△ABD ,所以S△AMB=
,所以S△AMB= S△ABE,
S△ABE,在平行四边形中,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半
故△ABM与△ABC的面积比=
 =
= .
.故答案为:
 .
.点评:本题考查向量知识的运用,考查三角形面积的计算,解题的关键是确定三角形的面积,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
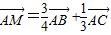 ,则S△ABM:S△ABC等于( )
,则S△ABM:S△ABC等于( )


