题目内容
若点M是△ABC所在平面内一点,且满足
=
+
,则S△ABM:S△ABC等于( )
| AM |
| 3 |
| 4 |
| AB |
| 1 |
| 3 |
| AC |
分析:本题考查的知识点是向量在几何中的应用,及三角形面积的性质,由△ABM与△ABC为同底不等高的三角形,故高之比即为两个三角面积之间,连接CM并延长后,我们易得到CM与CD长度的关系,进行得到△ABM的面积与△ABC面积之比.
解答: 解:连接CM并延长,交AB于D,
解:连接CM并延长,交AB于D,
则
=
+
=
+
,
即
=2
,
故
=
,
则△ABM的面积与△ABC面积之比为
.
故选B.
 解:连接CM并延长,交AB于D,
解:连接CM并延长,交AB于D,则
| AM |
| 3 |
| 4 |
| AB |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AC |
即
| CM |
| PD |
故
| CD |
| 1 |
| 3 |
| PD |
则△ABM的面积与△ABC面积之比为
| 1 |
| 3 |
故选B.
点评:三角形面积性质:同(等)底同(等)高的三角形面积相等;同(等)底三角形面积这比等于高之比;同(等)高三角形面积之比等于底之比.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
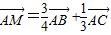 ,则S△ABM:S△ABC等于( )
,则S△ABM:S△ABC等于( )


