题目内容
若点M是△ABC所在平面内的一点,且满足
=
+
,则△ABM与△ABC面积之比等于
| AM |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
1:4
1:4
.分析:欲求△ABM的面积与△ABC面积之比,而这两个三角形同底只需求高之比即可,过C作AB的垂线交AB与点D,过点M作AB的垂线交AB与点E,取AH=
AC,AN=
AB,过点H作AB的垂线交AB与点F,可得S△ABM:S△ABC=ME:CD=HF:CD=AH:AC,得到结论.
| 1 |
| 4 |
| 3 |
| 4 |
解答:解:∵
=
+
,
∴M,B,C 三点共线
过C作AB的垂线交AB与点D,过点M作AB的垂线交AB与点E
取AH=
AC,AN=
AB,过点H作AB的垂线交AB与点F
∵
=
+
,
∴
=
+
即AHMN构成平行四边形,则HF=ME
而S△ABM:S△ABC=ME:CD=HF:CD=AH:AC=
∴△ABM的面积与△ABC面积之比为1:4.
故答案为:1:4.
| AM |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |

∴M,B,C 三点共线
过C作AB的垂线交AB与点D,过点M作AB的垂线交AB与点E
取AH=
| 1 |
| 4 |
| 3 |
| 4 |
∵
| AM |
| 3 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
∴
| AM |
| AH |
| AN |
而S△ABM:S△ABC=ME:CD=HF:CD=AH:AC=
| 1 |
| 4 |
∴△ABM的面积与△ABC面积之比为1:4.
故答案为:1:4.
点评:本题主要考查了向量在几何中的应用,解题的关键利用同(等)底三角形面积这比等于高之比,属于中档题.

练习册系列答案
相关题目
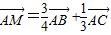 ,则S△ABM:S△ABC等于( )
,则S△ABM:S△ABC等于( )


