题目内容
对于定义域为D的函数y=f(x),若同时满足:①f(x)在D内单调递增或单调递减;②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].那么把函数y=f(x)(x∈D)叫做“同族函数”.
(1)求“同族函数”y=x2(x≥0)符合条件②的区间[a,b].
(2)是否存在实数k,使函数y=k+
是“同族函数”?若存在,求实数k的取值范围;若不存在,请说明理由.
(1)求“同族函数”y=x2(x≥0)符合条件②的区间[a,b].
(2)是否存在实数k,使函数y=k+
| x+2 |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:(1)由题意,函数f(x)=x2在[a,b]上单调递增,从而得
从而求得.
(2)假设函数y=k+
是“同族函数”,从而得到
,从而得方程x2-(2k+1)x+k2-2=0 (x≥-2,x≥k)有两个不相等的实数根;记f(x)=x2-(2k+1)x+k2-2,讨论以确定实数k的取值范围.
|
(2)假设函数y=k+
| x+2 |
|
解答:
解:(1)由题意,函数f(x)=x2在[a,b]上单调递增,
则
,解得
即所求的区间为[0,1].
(2)若函数y=k+
是“同族函数”,
则存在区间[a,b],在区间[a,b]上,函数y=f(x)的值域为[a,b].
而函数y=k+
在定义域内单调递增,
所以
,
则a,b是关于x的方程x=k+
的两个实数根,
即方程x2-(2k+1)x+k2-2=0 (x≥-2,x≥k)有两个不相等的实数根.
记f(x)=x2-(2k+1)x+k2-2,
当k≤-2时,有
解得-
<k≤-2.
当k>-2时,有
无解.
综上所述,实数k的取值范围是(-
,-2].
则
|
|
即所求的区间为[0,1].
(2)若函数y=k+
| x+2 |
则存在区间[a,b],在区间[a,b]上,函数y=f(x)的值域为[a,b].
而函数y=k+
| x+2 |
所以
|
则a,b是关于x的方程x=k+
| x+2 |
即方程x2-(2k+1)x+k2-2=0 (x≥-2,x≥k)有两个不相等的实数根.
记f(x)=x2-(2k+1)x+k2-2,
当k≤-2时,有
|
| 9 |
| 4 |
当k>-2时,有
|
综上所述,实数k的取值范围是(-
| 9 |
| 4 |
点评:本题考查了学生对新定义的接受能力及其应用,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
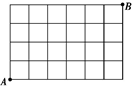 某市新城区有7条南北向街道,5条东西向街道(如图).
某市新城区有7条南北向街道,5条东西向街道(如图).