题目内容
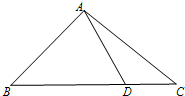
在△ABC中,B(-3,0),C(3,0),且∠ABC+∠ACB=135°,当顶点A在x轴上方时,求顶点A的轨迹方程.分析:由已知,∠BAC=45°,设A(x,y),用坐标表示出边AB,AC的长度,用余弦定理建立方程即可求出点A的轨迹方程.
解答:解:由∠ABC+∠ACB=135°,得,∠BAC=45°,设A(x,y),(y>0)则
|AB|=
,|AC|=
,|BC|=6
由余弦定理得
|BC|2=|AC|2+|AB|2-2|AB||AC|cos∠BAC
即62=(x+3)2+y2+(x-3)2+y2-2×
×
×
整理得x4+y4+18x2-18y2+2x2y2+81=0),(y>0)
答:顶点A的轨迹方程为x4+y4+18x2-18y2+2x2y2+81=0),(y>0).
|AB|=
| (x+3)2+y2 |
| (x-3)2+y2 |
由余弦定理得
|BC|2=|AC|2+|AB|2-2|AB||AC|cos∠BAC
即62=(x+3)2+y2+(x-3)2+y2-2×
| (x+3)2+y2 |
| (x-3)2+y2 |
| ||
| 2 |
整理得x4+y4+18x2-18y2+2x2y2+81=0),(y>0)
答:顶点A的轨迹方程为x4+y4+18x2-18y2+2x2y2+81=0),(y>0).
点评:本题考查实际问题中建立方程的方法,三角形中,建立方程的方法常用正弦定理与余弦定理.运算较繁,且最后方程不能化简成美观的形式.给解题者确定答案的正确性带来了难度.

练习册系列答案
相关题目
在△ABC中,∠B=90°,AC=
,D,E两点分别在AB,AC上.使
=
=2,DE=3.将△ABC沿DE折成直二面角,则二面角A-EC-B的余弦值为( )
| 15 |
| 2 |
| AD |
| DB |
| AE |
| EC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,∠B=
,三边长a,b,c成等差数列,且a,
,c成等比数列,则b的值是( )
| π |
| 3 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|