Question

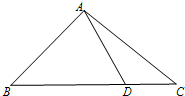
在△ABC中，∠B=90°，AC=

15

2

，D，E两点分别在AB，AC上．使

AD

DB

=

AE

EC

=2，DE=3．将△ABC沿DE折成直二面角，则二面角A-EC-B的余弦值为（　　）

• A、

  3 22

  22

• B、

  5 22

  22

• C、

  3 34

  34

• D、

  5 34

  34

Answer 1

分析：由已知中B=90°，AC=

15

2

，D，E两点分别在AB，AC上．使

AD

DB

=

AE

EC

=2，A-DE-B是直二面角，可得AD⊥底面DBCE，过D作DF⊥CE，交CE的延长线于F，连接AF，则∠AFD为二面角A-EC-B的平面角，解Rt△DFE即可求出二面角A-EC-B的余弦值．

解答：解：∵

AD

DB

=

AE

EC

=2，
∴DE∥BC，
又∵∠B=90°，
∴AD⊥DE．
∵A-DE-B是直二面角，AD⊥DE，故AD⊥底面DBCE，
过D作DF⊥CE，交CE的延长线于F，连接AF．
由三垂线定理知AF⊥FC，
故∠AFD为二面角A-EC-B的平面角．
在底面DBCE中，∠DEF=∠BCE，DB=2，EC=

5

2

，
∴sin∠BCE=

DB

EC

=

4

5

．
在Rt△DFE中，DE=3，
DF=DEsin∠DEF=DEsin∠BCE=

12

5

．
在Rt△AFD中，AD=4，cos∠AFD=

DF

AF

=

3 34

34

故选C

点评：本题考查的知识点是二面角的平面角及求法，其中确定∠AFD为二面角A-EC-B的平面角，将二面角问题转化为解三角形问题是解答本题的关键．