题目内容

函数y=cosx•sin（x+
π2
）的最小正周期是
 
分析：先用和差化积公式对函数关系式进行化简，进而根据T=
2π
w
求得函数最小正周期．
解答：解：y=cosx•sin（x+
π
2
）=
1
2
[sin（2x+
π
2
）-sin（-
π
2
）]=
1
2
cos2x+
1
2

∴T=
2π
2
=π
故答案为π
点评：本题主要考查了三角函数的周期性及其求法．解题的关键是先对函数式进行化简整理，进而根据T=
2π
w
求得最小正周期．
练习册系列答案
相关题目
在函数y=cosx，x∈[-
π
2
，
π
2
]的图象上有一点P（t，cost），此函数与x轴及直线x=t围成图形（如图阴影部分）的面积为S，则S 关于t的函数关系S=g（t）的图象可表示为（　　）
已知f（x）=2sinx（cosx-sinx），其中x∈R
（1）求函数f（x）的最小正周期，并从下列的变换中选择一组合适变换的序号，经过这组变换的排序，可以把函数y=sin2x的图象变成y=f（x）的图象；（要求变换的先后顺序）
①纵坐标不变，横坐标变为原来的
1
2
倍，
②纵坐标不变，横坐标变为原来的2倍，
③横坐标不变，纵坐标变为原来的
2
倍，
④横坐标不变，纵坐标变为原来的
2
2
倍，
⑤向上平移一个单位，⑥向下平移一个单位，
⑦向左平移
π
4
个单位，⑧向右平移
π
4
个单位，
⑨向左平移
π
8
个单位，⑩向右平移
π
8
个单位，
（2）在△ABC中角A，B，C对应边分别为a，b，c，f（A）=0，b=4，S△ABC=6，求a的长．
在函数y=cosx，x∈[-
π
2
，
π
2
]的图象上有一点P（t，cost），此函数图象与x轴及直线x=t围成图形（如图阴影部分）的面积为S，则S关于t的函数关系S=g（t）的图象可以是（　　）
（2011•顺义区二模）已知定义在区间[0，
3π
2
]上的函数y=f（x）的图象关于直线x=
3π
4
对称，当x≥
3π
4
时，f（x）=cosx，如果关于x的方程f（x）=a有解，记所有解的和为S，则S不可能为（　　）
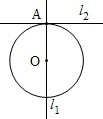（2013•江西）如图．已知l1⊥l2，圆心在l1上、半径为1m的圆O在t=0时与l2相切于点A，圆O沿l1以1m/s的速度匀速向上移动，圆被直线l2所截上方圆弧长记为x，令y=cosx，则y与时间t（0≤t≤1，单位：s）的函数y=f（t）的图象大致为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网