题目内容
已知函数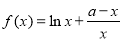 ,其中
,其中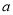 为常数,且
为常数,且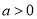 .
.
(I)若曲线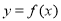 在点
在点 处的切线与直线
处的切线与直线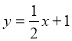 垂直,求
垂直,求 的值;
的值;
(II)若函数 在区间
在区间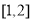 上的最小值为
上的最小值为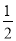 ,求
,求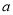 的值.
的值.
(I)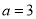 ;(II)
;(II)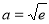 .
.
【解析】
试题分析:(I)首先对函数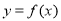 求导,当
求导,当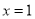 时的导函数即为曲线
时的导函数即为曲线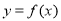 在点
在点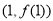 处的切线的斜率,且直线
处的切线的斜率,且直线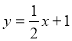 垂直,所以
垂直,所以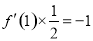 ,进而得到关于
,进而得到关于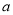 的方程,求得其值;(II)根据
的方程,求得其值;(II)根据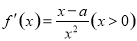 对
对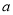 分情况讨论:当
分情况讨论:当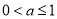 时,当
时,当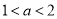 时,当
时,当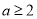 时,分别讨论其最小值,进而求得
时,分别讨论其最小值,进而求得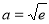 .
.
试题解析: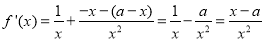 (
(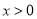 ) 2分
) 2分
(I)因为曲线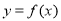 在点(1,
在点(1,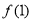 )处的切线与直线
)处的切线与直线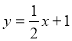 垂直,
垂直,
所以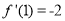 ,即
,即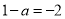 ,解得
,解得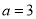 4分
4分
(II)当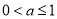 时,
时,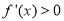 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时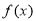 在[1,2]上为增函数,
在[1,2]上为增函数,
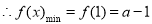 . 6分
. 6分
当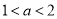 时,由
时,由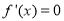 得,
得,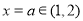 ,
,
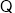 当
当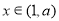 有
有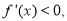
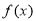 在[1,a]上为减函数,
在[1,a]上为减函数,
当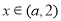 有
有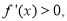
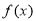 在[a,2]上为增函数,
在[a,2]上为增函数,
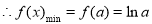 . 8分
. 8分
当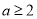 时,
时,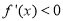 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时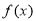 在[1,2]上为减函数,
在[1,2]上为减函数,
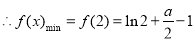 . 10分
. 10分
于是,①当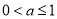 时,
时,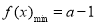
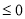 ; 11分
; 11分
②当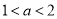 时,
时,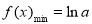 ,令
,令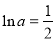 ,得
,得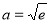 ;
;
③当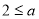 时,
时,
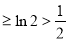 .
.
综上所述,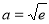 .……12分
.……12分
考点:1.利用导函数求切线斜率;2.分类讨论思想;3.利用求导得到函数最值.

练习册系列答案
相关题目

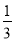 C.
C.  D.
D. 
 的平均数为
的平均数为 ,则该组样本数据的方差为
,则该组样本数据的方差为  的图像向左平移个
的图像向左平移个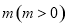 单位长度后,所得的图像关于
单位长度后,所得的图像关于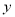 轴对称,则
轴对称,则 的最小值是
的最小值是  ,
, ,则
,则
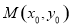 为抛物线
为抛物线
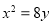 上一点,
上一点,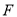 为抛物线
为抛物线 的焦点,以
的焦点,以 为半径的圆和抛物线
为半径的圆和抛物线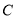 的准线相交,则
的准线相交,则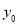 的取值范围是 。
的取值范围是 。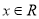 ,
,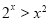 ;
; 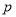 且
且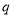 ”为假命题,则
”为假命题,则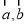 的夹角是钝角”的充分不必要条件是“
的夹角是钝角”的充分不必要条件是“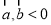 ”;
”;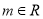 ,使
,使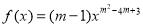 是幂函数,且在
是幂函数,且在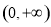 上是递减的.
上是递减的.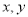 满足约束条件
满足约束条件 ,若目标函数
,若目标函数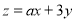 仅在点(1,0)处取得最小值,则a的取值范围为_________.
仅在点(1,0)处取得最小值,则a的取值范围为_________.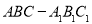 中,点
中,点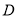 是
是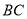 的中点,
的中点,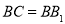 .
.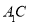 ∥平面
∥平面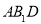 ;
;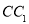 上找一点
上找一点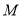 ,使
,使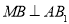 .
.