题目内容
18．若函数f（x）唯一的零点同时在（1，1.5），（1.25，1.5），（1.375，1.5），（1.4375，1.5）内，则该零点（精确度为0.01）的一个近似值约为（ ）| A． | 1.02 | B． | 1.27 | C． | 1.39 | D． | 1.45 |
分析 根据二分法的定义以及精确度为即可判断．
解答 解：由图中参考数据可得f（1.4375）•f（1.5）＜0，又因为题中要求精确到0.01，
所以近似值为 1.45
故选D．
点评 本题本题主要考查用二分法求区间根的问题，属于基础题型．在利用二分法求区间根的问题上，如果题中有根的精确度的限制，在解题时就一定要计算到满足要求才能结束．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
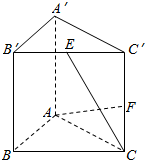在直三棱柱ABC-A′B′C′中，AB=AC=2，AA′=3，AB⊥AC，E为棱B′C′的中点，F为侧棱CC′上一点，若CE⊥AF，则AF与平面ABB′A′所成的角的正切值为（ ）
在直三棱柱ABC-A′B′C′中，AB=AC=2，AA′=3，AB⊥AC，E为棱B′C′的中点，F为侧棱CC′上一点，若CE⊥AF，则AF与平面ABB′A′所成的角的正切值为（ ）| A． | 3 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{4}{3}$ |
3．
阅读如图所示程序框图，根据框图的算法功能回答下列问题：
（Ⅰ）当输入的x∈[-1，3]时，求输出y的值组成的集合；
（Ⅱ）已知输入的x∈[a，b]时，输出y的最大值为8，最小值为3，求实数a，b的值．
阅读如图所示程序框图，根据框图的算法功能回答下列问题：（Ⅰ）当输入的x∈[-1，3]时，求输出y的值组成的集合；
（Ⅱ）已知输入的x∈[a，b]时，输出y的最大值为8，最小值为3，求实数a，b的值．
10．已知椭圆$\frac{x^2}{9}+\frac{y^2}{n^2}=1$与双曲线$\frac{x^2}{4}-\frac{y^2}{m^2}=1$有相同的焦点，则动点P（n，m）的轨迹是（ ）
| A． | 椭圆的一部分 | B． | 双曲线的一部分 | C． | 抛物线的一部分 | D． | 圆的一部分 |