题目内容
18.(B组题)设定义在R上的奇函数y=f(x)满足:对任意的x∈R,总有f(x-4)=f(x+4),且当x∈(0,4)时,$f(x)={e^{x-\frac{π}{2}}}+|{cosx}|-2$.则函数f(x)在区间[-8,16)上的零点个数是( )| A. | 6 | B. | 9 | C. | 12 | D. | 13 |
分析 作出y=e${\;}^{x-\frac{π}{2}}$和y=2-|cosx|的函数图象,根据图象得出f(x)在(0,4)上的零点个数,再根据奇函数的性质可知f(x)在一个周期内有3个零点,从而得出答案.
解答 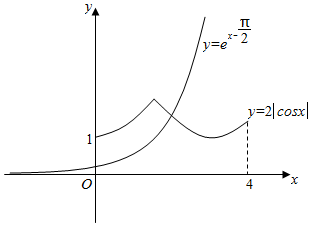 解:∵f(x-4)=f(x+4),∴f(x)的周期为8,
解:∵f(x-4)=f(x+4),∴f(x)的周期为8,
令e${\;}^{x-\frac{π}{2}}$+|cosx|-2=0可得e${\;}^{x-\frac{π}{2}}$=2-|cosx|,
作出y=e${\;}^{x-\frac{π}{2}}$和y=2-|cosx|的函数图象如图所示:
由图象可知f(x)在(0,4)上有1个零点,
∵f(x)是奇函数,∴f(x)在(-4,0)上有1个零点,
又f(0)=0,∴f(x)在(-4,4)上有3个零点,
∵f(x)在一个周期内有3个零点,
∴f(x)在[-8,16)上有9个零点.
故选B.
点评 本题考查了函数的零点与函数图象的关系,奇函数的性质,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.运行如下程序框图,分别输入t=45,t=-$\frac{172}{3}$,则输出s的和为( )


| A. | -2017 | B. | 2017 | C. | -2016 | D. | 2016 |
6.有一回归方程为$\hat y$=2-5x,当x增加一个单位时( )
| A. | y平均增加2个单位 | B. | y平均增加5个单位 | ||
| C. | y平均减少2个单位 | D. | y平均减少5个单位 |
3.刘老师是一位经验丰富的高三理科班班主任,经长期研究,他发现高中理科班的学生的数学成绩(总分150分)与理综成绩(物理、化学与生物的综合,总分300分)具有较强的线性相关性,以下是刘老师随机选取的八名学生在高考中的数学得分x与理综得分y(如表):
参考数据及公式:$\widehaty=a+bx,b=\frac{{{x_1}{y_1}+{x_2}{y_2}+…+{x_n}{y_n}-n\overline x\overline y}}{{x_1^2+x_2^2+…+x_n^2-n{{\overline x}^2}}}≈1.83,\overline x=100,\overline y=200$.
(1)求出y关于x的线性回归方程;
(2)若小汪高考数学110分,请你预测他理综得分约为多少分?(精确到整数位);
(3)小金同学的文科一般,语文与英语一起能稳定在215分左右.如果他的目标是在高考总分冲击600分,请你帮他估算他的数学与理综大约分别至少需要拿到多少分?(精确到整数位).
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
| 理综分数y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
(1)求出y关于x的线性回归方程;
(2)若小汪高考数学110分,请你预测他理综得分约为多少分?(精确到整数位);
(3)小金同学的文科一般,语文与英语一起能稳定在215分左右.如果他的目标是在高考总分冲击600分,请你帮他估算他的数学与理综大约分别至少需要拿到多少分?(精确到整数位).
7.设复数z=3-2i,则z的虚部是( )
| A. | i | B. | 3 | C. | 2 | D. | -2 |
14.已知某一随机变量X的概率分布列如下,求E(X)=7
| X | 1 | 5 | 9 |
| P | 0.1 | 0.3 | a |