题目内容
已知等差数列{an}公差不为0,且a3=5,a1,a2,a5成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+2b2+22b3+…+2n-1bn=an,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+2b2+22b3+…+2n-1bn=an,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)在等差数列{an}中,设其公差为d,(d≠0),依题意可得(5-2d)(5+2d)=(5-d)2,解之可求得d,从而可得数列{an}的通项公式;
(2)由b1+2b2+22b3+…+2n-1bn=an,可得b1+2b2+22b3+…+2n-1bn+2nbn+1=an+1,两式相减得:2nbn+1=2,可求得bn,继而可求得bn的前n项和Tn.
(2)由b1+2b2+22b3+…+2n-1bn=an,可得b1+2b2+22b3+…+2n-1bn+2nbn+1=an+1,两式相减得:2nbn+1=2,可求得bn,继而可求得bn的前n项和Tn.
解答:
解:(1)在等差数列{an}中,设其公差为d,(d≠0),
∵a1a5=a22,a3=5,∴(a3-2d)(a3+2d)=a22,即(5-2d)(5+2d)=(5-d)2,…2分
化简得5d2-10d=0,
∴d=2…4分
∴an=a3+(n-3)d=5+2(n-3)=2n-1…7分
(2)∵b1+2b2+22b3+…+2n-1bn=an,①
∴b1+2b2+22b3+…+2n-1bn+2nbn+1=an+1,②
②-①得:2nbn+1=2,
∴bn+1=21-n…10分
当n=1时,b1=a1=1,
∴bn=
…12分
∴Tn=b1+b2+b3+…+bn=1+1+
+
+…+
=1+
=3-
…14分
∵a1a5=a22,a3=5,∴(a3-2d)(a3+2d)=a22,即(5-2d)(5+2d)=(5-d)2,…2分
化简得5d2-10d=0,
∴d=2…4分
∴an=a3+(n-3)d=5+2(n-3)=2n-1…7分
(2)∵b1+2b2+22b3+…+2n-1bn=an,①
∴b1+2b2+22b3+…+2n-1bn+2nbn+1=an+1,②
②-①得:2nbn+1=2,
∴bn+1=21-n…10分
当n=1时,b1=a1=1,
∴bn=
|
∴Tn=b1+b2+b3+…+bn=1+1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22-n |
1-(
| ||
1-
|
| 1 |
| 2n-2 |
点评:本题考查数列的求和,着重考查等比数列的性质与求和公式的应用,考查运算求解能力,属于难题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
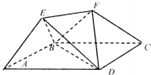 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD= 有若干个棱长为1的正方体搭成的几何体主视图与侧视图相同(如图所示),则搭成该几何体体积的最大值与最小值的和等于
有若干个棱长为1的正方体搭成的几何体主视图与侧视图相同(如图所示),则搭成该几何体体积的最大值与最小值的和等于