题目内容
已知函数 ,设
,设 在点
在点 N*)处的切线在
N*)处的切线在 轴上的截距为
轴上的截距为 ,数列
,数列 满足:
满足: N*).
N*).
(1)求数列 的通项公式;
的通项公式;
(2)在数列 中,仅当
中,仅当 时,
时, 取最小值,求
取最小值,求 的取值范围;
的取值范围;
(3)令函数 ,数列
,数列 满足:
满足: ,
, N*),
N*),
求证:对于一切 的正整数,都满足:
的正整数,都满足: .
.
解:(1)
 ,则
,则 ,
,
得 ,即
,即 ,
,
∴数列 是首项为2、公差为1的等差数列,
是首项为2、公差为1的等差数列,
∴ ,即
,即 . …4分
. …4分
(2) ,∴函数
,∴函数 在点
在点 N*)处的切线方程为:
N*)处的切线方程为:
 ,令
,令 ,得
,得 .
.
 ,仅当
,仅当 时取得最小值,
时取得最小值,
只需 ,解得
,解得 ,故
,故 的取值范围为
的取值范围为 .…8分
.…8分
(3) ,故
,故 ,
,

 ,故
,故 ,则
,则 ,即
,即 .
.
∴
= .
.
又
 ,
,
故 . …13分
. …13分

练习册系列答案
相关题目

 中,平面
中,平面 与平面
与平面 所成的锐二面角的大小是 .
所成的锐二面角的大小是 .
 ,
, 是由
是由 轴和曲线
轴和曲线 及该曲线在点
及该曲线在点 处的切线所围成的封闭区域,则
处的切线所围成的封闭区域,则 在
在 B.
B. C.1 D.2
C.1 D.2  为不超过实数
为不超过实数 ,
, 。设
。设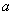 为正整数,数列
为正整数,数列 满足
满足 ,
, ,现有下列命题:
,现有下列命题: 时,数列
时,数列 ,当
,当 时总有
时总有 ;
; 时,
时, ;
; ,则当
,则当 。
。 π B.2π
π B.2π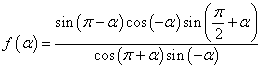 .
.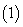 化简
化简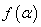 ;
; 若角
若角 是
是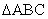 的内角,且
的内角,且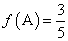 ,求
,求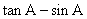 的值.
的值.