题目内容
17．在△ABC中，已知a=1，b=2，C=60°，求c，B．分析 由题意和余弦定理可得c值，再由勾股定理可得B值
解答 解：∵在△ABC中a=1，b=2，C=60°，
∴由余弦定理可得c2=12+22-2×1×2×cos60°=3，
∴c=$\sqrt{3}$，满足a2+c2=b2，∴B=90°．
点评 本题考查余弦定理解三角形，涉及勾股定理，属基础题．
练习册系列答案
相关题目
如果在四棱锥P-ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，G为AD边的中点，求证：BG⊥PA．
12．若tanα+cotα=4，则sin2α=（ ）
| A． | -$\frac{1}{4}$ | B． | $\frac{1}{4}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
6．若奇函数y=g（x）与f（x）=2sin（2x+φ）图象关于直线x=$\frac{π}{6}$对称，要得到y=g（x），则可用y=f（x）的图象变换得到（|φ|＜$\frac{π}{2}$），需经过的变换是（ ）
| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
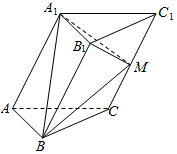在三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，M为CC1的中点，∠ABC=90°，AC=A1A，∠A1AC=60°，AB=BC=2．