题目内容
已知空间四边形ABCD中,M、N分别为AB、CD的中点,求MN与
的大小关系.
| AC+BD |
| 2 |
考点:向量在几何中的应用
专题:解三角形
分析:取BC中点H,连结MH,NH,MN,由三角形中位线定理和三角形三边关系能推导出MN<
.
| AC+BD |
| 2 |
解答:
 解:取BC中点H,连结MH,NH,MN,
解:取BC中点H,连结MH,NH,MN,
∵M、N分别为AB、CD的中点,
∴MH=
AC,NH=
BD,
∵在△HMN中,MH+NH>MN,
∴MN<
.
 解:取BC中点H,连结MH,NH,MN,
解:取BC中点H,连结MH,NH,MN,∵M、N分别为AB、CD的中点,
∴MH=
| 1 |
| 2 |
| 1 |
| 2 |
∵在△HMN中,MH+NH>MN,
∴MN<
| AC+BD |
| 2 |
点评:本题考查三角形中三边关系的应用,是中档题,解题时要注意三角形中位线定理的合理运用.

练习册系列答案
相关题目
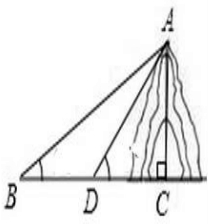 如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=
如图,从B处看山顶A的仰角为45°,向前100米,在D处看山顶A的仰角为60°,求:山AC的高度(已知sin15°=