题目内容
已知在△ABC中，内角A，B，C的对边长分别是a，b，c，若a•
+b•
+c•
=0．求证：△ABC是等边三角形．
| BC |
| CA |
| AB |
考点：三角形的形状判断
专题：解三角形
分析：由条件可得
•（|
|-|
|）+
•（|
|-|
|）．再根据
和
不共线，可得|
|-|
|=0，|
|-|
|=0，由此证得结论．
| BC |
| BC |
| AB |
| CA |
| CA |
| AB |
| BC |
| CA |
| BC |
| AB |
| CA |
| AB |
解答：
证明：在△ABC中，∵a•
+b•
+c•
=0，∴|
|•
+|
|•
+|
|•（
+
）=0，
化简可得
•（|
|-|
|）+
•（|
|-|
|）．
∵
和
不共线，∴|
|-|
|=0，|
|-|
|=0，即|
|-|
|=|
|，
故：△ABC是等边三角形．
| BC |
| CA |
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| AC |
| CB |
化简可得
| BC |
| BC |
| AB |
| CA |
| CA |
| AB |
∵
| BC |
| CA |
| BC |
| AB |
| CA |
| AB |
| BC |
| AB |
| CA |
故：△ABC是等边三角形．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量不共线的性质，属于基础题．
练习册系列答案
相关题目
若p：?x∈R，sinx≤1，则（ ）
| A、?p：?x∈R，sinx＞1 |
| B、?p：?x∈R，sinx＞1 |
| C、?p：?x∈R，sinx≥1 |
| D、?p：?x∈R，sinx≥1 |
在△ABC中，已知sinA：sinB：sinC=5：7：8，则∠B的大小为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
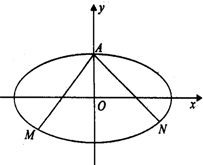如图已知椭圆