题目内容

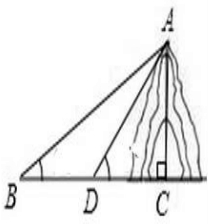如图，从B处看山顶A的仰角为45°，向前100米，在D处看山顶A的仰角为60°，求：山AC的高度（已知sin15°=
6
-
2
4
，cos15°=
6
+
2
4
）
考点：解三角形的实际应用
专题：解三角形
分析：利用任意角的三角函数，求出山高与BD的关系，即可求出山高．
解答： 解：从B处看山顶A的仰角为45°，∴AC=BC，
向前100米，在D处看山顶A的仰角为60°，∴DC=AC-100．
tan∠ADC=
AC
DC
=
AC
AC-100
=tan60°=
3
．
解得AC=
100
3
3
-1
=50（
3
+3） （米）．
山AC的高度：50（
3
+3） （米）．
点评：本题考查三角形的解法，任意角的三角函数，基本知识的考查．
练习册系列答案
相关题目
若sin(π-α)=-2sin(
π
2
+α)，则sinα•cosα=（　　）
A、
2
5
B、-
1
5
C、-
2
5
D、
2
5
或-
2
5
设
a
=(
3
2
，sinα)，
b
=(cosα，
1
3
)，且
a
∥
b
，则锐角α为
 
．
设F1，F2为双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，过坐标原点O的直线与双曲线C在第一象限内交于点P，若|PF1|+|PF2|=6a，且△PF1F2为锐角三角形，则直线OP斜率的取值范围是（　　）
A、(
2
3
3
，
4
3
)
B、(
4
3
，
3
)
C、(1，
2
3
3
)
D、(
2
3
3
，
2
)
已知函数f（x）=
2x-1
2x+1
（x∈R）
（1）判断函数f（x）的奇偶性；
（2）若对任意的x∈R，都有不等式f（2x）+f（x2-m）＞0恒成立，求实数m的取值范围．
已知函数f（x）=x2+（a+2）x+b，满足f（-1）=-2；
（1）若方程f（x）=2x有唯一的解，求实数a，b的值；
（2）若函数f（x）在区间[-3，2]上不是单调函数，求实数a的取值范围．
已知空间四边形ABCD中，M、N分别为AB、CD的中点，求MN与
AC+BD
2
的大小关系．
是否存在数列{bn}使得（2b1-n）C
 
1
n
+（2b2-n）C
 
2
n
+（2b3-n）C
 
3
n
+…+（2bn-n）C
 
n
n
=n对一切n∈N*成立？若存在，求数列{bn}的通项公式；若不存在，请说明理由．
已知函数f（x）=lnx+ax+
a+1
x
+3（a∈R）．
（1）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）当a=1时，若关于x的不等f（x）≥m2-5m恒成立，求实数m的取值范围；
（3）当a≥-
1
2
时，讨论f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网