题目内容
设f(n)= +
+ +…+
+…+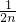 (n∈N),则f(n+1)-f(n)=________.
(n∈N),则f(n+1)-f(n)=________.
 -
-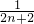
分析:利用f(n)=
 +
+ +…+
+…+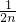 (n∈N),计算f(n+1)-f(n)即可.
(n∈N),计算f(n+1)-f(n)即可.解答:∵f(n)=
 +
+ +…+
+…+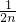 (n∈N),
(n∈N),∴f(n+1)=
 +
+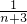 +…+
+…+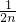 +
+ +
+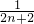 ,
,∴f(n+1)-f(n)=(
 +
+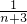 +…+
+…+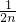 +
+ +
+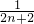 )-(
)-( +
+ +…+
+…+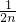 )
)=
 +
+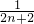 -
-
=
 -
-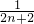 .
.故答案为:
 -
-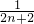 .
.点评:本题考查函数的表示方法,明确从n到n+1项数的变化是关键,属于基础题.

练习册系列答案
相关题目
