题目内容
设对于任意的实数x,y,函数f(x),g(x)满足f(x+1)=| 1 |
| 3 |
n∈R+
(Ⅰ)求数列{f(n)}和{g(n)}的通项公式;
(Ⅱ)设Cn=g[
| n |
| 2 |
(Ⅲ)设F(n)=Sn-3n,存在整数m和M,使得对任意正整数n不等式m<F(n)<M恒成立,求M-m的最小值.
分析:(Ⅰ)由题意可得:取x=n,得f(n+1)=
f(n),故数列{f(n)}等比数列,取x=n,y=1,得g(n+1)-g(n)=2,故数列{g(n)}是等差数列,进而得到答案.
(Ⅱ)由题意可得:Cn=n(
)n-1+3,然后利用错位相减的方法求出数列的前n项和为Sn=
+3n-
(
)n-1.
(Ⅲ)因为F(n)=Sn-3n,所以F(n)=Sn=
-
(
)n-1,利用增函数的定义判断出数列是增数列,所以F(n)的最小值为F(1)=1.由极限的思想可得F(n)<
,所以1≤F(n)<
.因此当m<1且M≥
时,不等式m<F(n)<M恒成立,进而得到答案.
| 1 |
| 3 |
(Ⅱ)由题意可得:Cn=n(
| 1 |
| 3 |
| 9 |
| 4 |
| 2n+3 |
| 4 |
| 1 |
| 3 |
(Ⅲ)因为F(n)=Sn-3n,所以F(n)=Sn=
| 9 |
| 4 |
| 2n+3 |
| 4 |
| 1 |
| 3 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
解答:解:(Ⅰ)由题意可得:取x=n,得f(n+1)=
f(n),取x=0,f(1)=
f(0)=1
故数列{f(n)}是首项是1,公比为
的等比数列,所以f(n)=(
)n-1.
取x=n,y=1,得g(n+1)=g(n)+2(n∈N),即g(n+1)-g(n)=2,
故数列{g(n)}是公差为2的等差数列,又g(5)=13,
所以g(n)=2n+3.
(Ⅱ)由题意可得:Cn=g[
f(n)]=n(
)n-1+3,
所以Sn;=1+2×
+3×(
)2+…+n×(
)n-1+3n…①
Sn=
+2×(
)2+3×(
)3+…+n×(
)n+n…②,
所以①-②可得:
Sn=1+
+(
)2+(
)3+…+(
)n-1-n×(
)n+2n=
[1-(
)n]-n(
)n+2n,
所以Sn=
+3n-
(
)n-1.
所以数列{Cn}的前项和Sn=
+3n-
(
)n-1.
(Ⅲ)因为F(n)=Sn-3n,
所以F(n)=Sn=
-
(
)n-1,
所以F(n+1)-F(n)=(n+1)(
)n>0
所以F(n)是单调递增数列,那么F(n)的最小值为F(1)=1.
由于当n→+∞时,
(
)n-1→0,所以当n→+∞时,F(n)→
,
因为
(
)n-1<0,所以F(n)<
,所以1≤F(n)<
.
因此当m<1且M≥
时,不等式m<F(n)<M恒成立,
所以存在正数m=0,-1,-2…;M=3,4,5…,使得对任意的正整数,不等式m<F(n)<M恒成立.
此时,M-m的最小值为3.
| 1 |
| 3 |
| 1 |
| 3 |
故数列{f(n)}是首项是1,公比为
| 1 |
| 3 |
| 1 |
| 3 |
取x=n,y=1,得g(n+1)=g(n)+2(n∈N),即g(n+1)-g(n)=2,
故数列{g(n)}是公差为2的等差数列,又g(5)=13,
所以g(n)=2n+3.
(Ⅱ)由题意可得:Cn=g[
| n |
| 2 |
| 1 |
| 3 |
所以Sn;=1+2×
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
所以①-②可得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
所以Sn=
| 9 |
| 4 |
| 2n+3 |
| 4 |
| 1 |
| 3 |
所以数列{Cn}的前项和Sn=
| 9 |
| 4 |
| 2n+3 |
| 4 |
| 1 |
| 3 |
(Ⅲ)因为F(n)=Sn-3n,
所以F(n)=Sn=
| 9 |
| 4 |
| 2n+3 |
| 4 |
| 1 |
| 3 |
所以F(n+1)-F(n)=(n+1)(
| 1 |
| 3 |
所以F(n)是单调递增数列,那么F(n)的最小值为F(1)=1.
由于当n→+∞时,
| 2n+3 |
| 4 |
| 1 |
| 3 |
| 9 |
| 4 |
因为
| 2n+3 |
| 4 |
| 1 |
| 3 |
| 9 |
| 4 |
| 9 |
| 4 |
因此当m<1且M≥
| 9 |
| 4 |
所以存在正数m=0,-1,-2…;M=3,4,5…,使得对任意的正整数,不等式m<F(n)<M恒成立.
此时,M-m的最小值为3.
点评:解决此类问题的关键是利用函数的赋值法求出数列的通项公式,数列掌握数列求出的方法以及求数列和的最值的方法,此题是数列与函数与不等式的综合题型属于难题.

练习册系列答案
相关题目
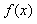 ,
,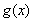 满足
满足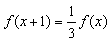 , 且f(0)=3,g(x+y)=g(x)+
, 且f(0)=3,g(x+y)=g(x)+ 和
和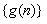 的通项公式;
的通项公式;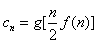 ,求数列
,求数列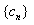 的前n项和Sn;
的前n项和Sn; 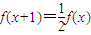 ,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式
,且f(0)=2,g(x+y)=g(x)+2y,g(3)=5,an=f(n),bn=g(n),n?N*. (Ⅰ)求数列an,bn的通项公式bn的通项公式