题目内容
4.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆面积为π,A,B两点的坐标分别为(x1,y1)和(x2,y2),则|y2-y1|的值为( )| A. | $\frac{5}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{10}{3}$ |
分析 由已知△ABF2内切圆半径r=1.,从而求出△ABF2,再由ABF2面积=$\frac{1}{2}$|y1-y2|×2c,能求出|y1-y2|.
解答 解:∵椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别为F1,F2,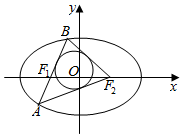
过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,
△ABF2的内切圆的面积为π,
∴△ABF2内切圆半径r=1.
△ABF2面积S=$\frac{1}{2}$×1×(AB+AF2+BF2)=2a=10,
∴ABF2面积=$\frac{1}{2}$|y1-y2|×2c=$\frac{1}{2}$|y1-y2|×2×3=10,
∴|y1-y2|=$\frac{10}{3}$.
故选:D.
点评 本题考查椭圆的简单性质,考查数学转化思想方法,是中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.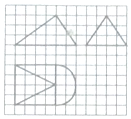 如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
 如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )
如图,网格纸上校正方形的边长为1,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )| A. | 16+4π | B. | 16+2π | C. | 48+4π | D. | 48+2π |
15.已知函f(x)数的导数f′(x)=3x2-3ax,f(0)=b,a,b为实数,1<a<2.若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,则a-b的值为$\frac{1}{3}$.
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
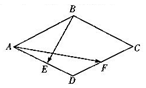

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
16.0<a<1是函数f(x)=2ax2+1取值恒为正的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
14.某程序框图如图所示,执行该程序,若输入4,则输出S=( )


| A. | 10 | B. | 17 | C. | 19 | D. | 36 |