题目内容
5.已知函数f(x)的定义域为[3,6],则函数$y=\frac{f(2x)}{{\sqrt{{{log}_{\frac{1}{2}}}(2-x)}}}$的定义域为[$\frac{3}{2},2$).分析 由f(x)的定义域求出f(2x)的定义域,再由分母中根式内部的对数式大于0求出x的范围,取交集得答案.
解答 解:由f(x)的定义域为[3,6],得3≤2x≤6,解得$\frac{3}{2}≤x≤3$.
由$lo{g}_{\frac{1}{2}}(2-x)>0$,得0<2-x<1,即1<x<2.
∴函数$y=\frac{f(2x)}{{\sqrt{{{log}_{\frac{1}{2}}}(2-x)}}}$的定义域为[$\frac{3}{2},2$).
故答案为:[$\frac{3}{2},2$).
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的处理方法,是基础题.

练习册系列答案
相关题目
20.已知命题p:“任意的x∈R,存在m∈R,4x-2x+1-m=0且命题¬p是真命题,则实数m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<-1 | D. | m≤-1 |
14.若函数f(x)在区间[-2,2]上的图象是一条连续不断的曲线,且函数f(x)在(-2,2)上仅有一个零点,则f(-2)•f(2)的符号是( )
| A. | 小于零 | B. | 大于零 | C. | 小于或大于零 | D. | 不能确定 |
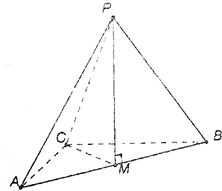 已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.
已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.