题目内容
10.设函数f(x)=ax+$\frac{1-x}{ax}$(a>0).求:利用函数单调性的定义,判断函数f(x)在 (0,+∞)上的单调性.
分析 先化简f(x)=ax+$\frac{1}{ax}$$-\frac{1}{a}$,根据单调性的定义判断f(x)在(0,+∞)上的单调性:设任意的x1>x2>0,然后作差,通分,提取公因式x1-x2,从而得到$f({x}_{1})-f({x}_{2})=({x}_{1}-{x}_{2})(a-\frac{1}{a{x}_{1}{x}_{2}})$,这样便可看出${x}_{1},{x}_{2}∈(0,\frac{1}{a})$,和${x}_{1},{x}_{2}∈(\frac{1}{a},+∞)$时,可以判断f(x1)与f(x2)的关系,从而判断出f(x)在(0,+∞)上的单调性.
解答 解:$f(x)=ax+\frac{1}{ax}-\frac{1}{a}$,设x1>x2>0,则:
$f({x}_{1})-f({x}_{2})=a{x}_{1}+\frac{1}{a{x}_{1}}-a{x}_{2}-\frac{1}{a{x}_{2}}$=$({x}_{1}-{x}_{2})(a-\frac{1}{a{x}_{1}{x}_{2}})$;
∵x1>x2>0,a>0;
∴x1-x2>0;
∴①${x}_{1},{x}_{2}∈(0,\frac{1}{a})$时,$a-\frac{1}{a{x}_{1}{x}_{2}}<0$;
∴f(x1)<f(x2);
∴f(x)在$(0,\frac{1}{a})$上单调递减;
②${x}_{1},{x}_{2}∈(\frac{1}{a},+∞)$时,$a-\frac{1}{a{x}_{1}{x}_{2}}>0$;
∴f(x1)>f(x2);
∴f(x)在[$\frac{1}{a}$,+∞)上单调递增.
点评 考查函数单调性的定义,根据单调性定义判断一个函数单调性的方法和过程,作差的方法比较f(x1),f(x2)的大小,作差之后,是分式的一般要通分,一般要提取公因式x1-x2.

| A. | f (2014)>f (2015)>f (2016) | B. | f (2016)>f (2014)>f (2015) | ||
| C. | f (2016)=f (2014)>f (2015) | D. | f (2014)>f (2015)=f (2016) |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
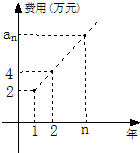 某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.