题目内容
设f(x)=2x-2-x.若当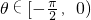 时,
时,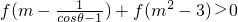 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是
- A.(-∞,-2)
- B.(-∞,-2]∪[1,+∞)
- C.(-2,1)
- D.(-∞,-2)∪(1,+∞)
D
分析:先判断f(x)的奇偶性、单调性,利用函数的性质把不等式中的符号“f”去掉,转化为具体不等式,进而把恒成立问题转化为函数最值解决即可.
解答:因为f(x)的定义域为R,且f(-x)=2-x-2x=-(2x-2-x)=-f(x),
所以f(x)为奇函数;
又易知f(x)=2x-2-x为增函数,
所以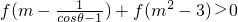 可化为f(
可化为f( )>-f(m2-3)=f(3-m2),
)>-f(m2-3)=f(3-m2),
也即m- >3-m2,即
>3-m2,即 在当
在当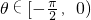 时恒成立,
时恒成立,
当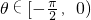 时,cosθ∈[0,1),
时,cosθ∈[0,1), ≤-1,
≤-1,
所以m2+m-3>-1,解得m<-2或m>1,即实数m的取值范围为(-∞,-2)∪(1,+∞).
故选D.
点评:本题考查函数的奇偶性、单调性及其应用,考查函数恒成立问题,考查学生分析问题解决问题的能力.
分析:先判断f(x)的奇偶性、单调性,利用函数的性质把不等式中的符号“f”去掉,转化为具体不等式,进而把恒成立问题转化为函数最值解决即可.
解答:因为f(x)的定义域为R,且f(-x)=2-x-2x=-(2x-2-x)=-f(x),
所以f(x)为奇函数;
又易知f(x)=2x-2-x为增函数,
所以
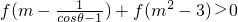 可化为f(
可化为f( )>-f(m2-3)=f(3-m2),
)>-f(m2-3)=f(3-m2),也即m-
 >3-m2,即
>3-m2,即 在当
在当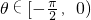 时恒成立,
时恒成立,当
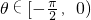 时,cosθ∈[0,1),
时,cosθ∈[0,1), ≤-1,
≤-1,所以m2+m-3>-1,解得m<-2或m>1,即实数m的取值范围为(-∞,-2)∪(1,+∞).
故选D.
点评:本题考查函数的奇偶性、单调性及其应用,考查函数恒成立问题,考查学生分析问题解决问题的能力.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目