题目内容
设f（x）=
，g（x）=
，下列四个结论
（1）f（2x）=2f（x）•g（x）； （2）g（2x）=2f（x）•g（x）；
（3）f（2x）=[f（x）]2+[g（x）]2； （4）g（2x）=[f（x）]2+[g（x）]2
中恒成立的个数有（ ）
| 2x-2-x |
| 2 |
| 2x+2-x |
| 2 |
（1）f（2x）=2f（x）•g（x）； （2）g（2x）=2f（x）•g（x）；
（3）f（2x）=[f（x）]2+[g（x）]2； （4）g（2x）=[f（x）]2+[g（x）]2
中恒成立的个数有（ ）
分析：根据函数f（x）、g（x）的解析式，利用多项式的乘法公式对各个选项中的等式加以验证，即可得到本题答案．
解答：解：对于（1），f（2x）=
，
∵f（x）•g（x）=
•
=
，
∴2f（x）•g（x）=2×
=
，得f（2x）=2f（x）•g（x），故（1）正确；
对于（2），由（1）的证明可得g（2x）≠2f（x）•g（x），故（2）不正确；
对于（3），f（x）=
，g（x）=
，
∴[f（x）]2+[g（x）]2=（
）2+（
）2=
=
∵f（2x）=
，∴f（2x）≠[f（x）]2+[g（x）]2，故（3）不正确；
对于（4），由（3）的证明可得g（2x）=
=[f（x）]2+[g（x）]2，故（4）正确
综上所述，正确的结论为（1）（4），共2个
故选：B
| 22x-2-2x |
| 2 |
∵f（x）•g（x）=
| 2x-2-x |
| 2 |
| 2x+2-x |
| 2 |
| 22x-2-2x |
| 4 |
∴2f（x）•g（x）=2×
| 22x-2-2x |
| 4 |
| 22x-2-2x |
| 2 |
对于（2），由（1）的证明可得g（2x）≠2f（x）•g（x），故（2）不正确；
对于（3），f（x）=
| 2x-2-x |
| 2 |
| 2x+2-x |
| 2 |
∴[f（x）]2+[g（x）]2=（
| 2x-2-x |
| 2 |
| 2x+2-x |
| 2 |
| 2•22x+2•2-2x |
| 4 |
| 22x+2-2x |
| 2 |
∵f（2x）=
| 22x-2-2x |
| 2 |
对于（4），由（3）的证明可得g（2x）=
| 22x+2-2x |
| 2 |
综上所述，正确的结论为（1）（4），共2个
故选：B
点评：本题给出函数f（x）、g（x）的解析式，判断几个等式的正确性．着重考查了基本初等函数、函数的对应法则和乘法公式等知识，属于中档题．
练习册系列答案
相关题目
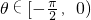时，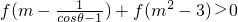
恒成立，则实数m的取值范围是