题目内容
设f(x)=
|
分析:根据函数解析式应先代入下面的式子求出f(5)的值,再代入对应的解析式求出f(f(5))的值.
解答:解:由题意知,f(x)=
,
则f(5)=log24=2,
∴f(f(5))=f(2)=22-2=1.
故答案为:1.
|
则f(5)=log24=2,
∴f(f(5))=f(2)=22-2=1.
故答案为:1.
点评:本题是分段函数求值问题,对应多层求值按“由里到外”的顺序逐层求值,一定要注意自变量的值所在的范围,然后代入相应的解析式求解.

练习册系列答案
相关题目
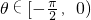 时,
时,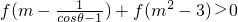 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是