题目内容

已知数列{an}满足a1=1，且
an+1
an
=
n+1
n
，则a2014=（　　）
A、2011B、2012
C、2013D、2014
考点：数列递推式
专题：等差数列与等比数列
分析：利用“累乘求积”即可得出．
解答： 解：∵数列{an}满足a1=1，且
an+1
an
=
n+1
n
，
∴an=
an
an-1
•
an-1
an-2
•…•
a2
a1
•a1
=
n
n-1
•
n-1
n-2
•…•
2
1
×1
=n，
∴a2014=2014．
故选：D．
点评：本题考查了“累乘求积”求数列的通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
数列{an}满足a1=1，a2=2，an+2=（1+cos2
nπ
2
）an+sin2
nπ
2
，n∈N*，{an}的前n项和为Sn，则S2n=
 
．
已知函数f（x）=x+
a
x
，且f（1）=3
（1）求a的值；
（2）判断函数f（x）在(
2
，+∞)上是增函数还是减函数？并证明．
设经过点（-4，0）的直线l与抛物线y=
1
2
x2的两个交点为A、B，经过A、B两点分别作抛物线的切线，若两切线互相垂直，则直线l的斜率等于
 
．
函数y=2sinx的单调增区间是（k∈Z）（　　）
A、[
π
2
+2kπ，
3π
2
+2kπ]
B、[-
π
2
+2kπ，
π
2
+2kπ]
C、[2kπ，π+2kπ]
D、[2kπ，
π
2
+2kπ]
已知函数f（x）为R上的奇函数，且当x＞0时，f（x）=x2+
1
x
，则函数f（x）的解析式为
 
．
已知f（x）=Asin（ωx+φ）+1（x∈R，A＞0，ω＞0，0＜φ＜
π
2
）的周期开为π，且图象上的一个最低点为M（
2π
3
，-1）．
（1）求f（x）的解析式；
（2）已知f（
α
2
）=
1
3
，α∈[0，π]，求cosα的值．
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（　　）
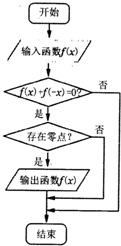
A、f（x）=
|x|
x
B、f（x）=
cosx
x
（-
π
2
＜x＜
π
2
，且x≠0）
C、f（x）=
2x-1
2x+1
D、f（x）=x2ln（x2+1）
已知数列{an}的通项an=
1
3
n3-
5
4
n2+3+m，若数列中的最小项为1，则m的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网