题目内容
已知O为坐标原点,
=(2cos2x+a,2sinx),
=(1,
cosx)(x∈R,a∈R,a是常数),设f(x)=
•
(1)求函数式f(x)关系式;
(2)已知函数f(x)在区间[0,
]上的最小值为-1,求a的值及函数f(x)的单调减区间.
| OA |
| OB |
| 3 |
| OA |
| OB |
(1)求函数式f(x)关系式;
(2)已知函数f(x)在区间[0,
| π |
| 2 |
考点:两角和与差的正弦函数,平面向量数量积的运算,正弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)由平面向量数量积的运算,两角和与差的正弦函数公式即可求得f(x)=1+a+2sin(2x+
).
(2)由x∈[0,
],可得2x+
∈[
,
],从而可求f(x)min=-1=f(
)=a,即可解得a的值,令2kπ+
≤2x+
≤2kπ+
,k∈Z可解得函数f(x)的单调减区间.
| π |
| 6 |
(2)由x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 7π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解答:
解:(1)f(x)=
•
=2cos2x+a+2
sinxcosx=1+a+cos2x+
sin2x=1+a+2sin(2x+
).
(2)∵x∈[0,
],
∴2x+
∈[
,
]
∴f(x)min=-1=f(
)=a
∴a=-1
∵令2kπ+
≤2x+
≤2kπ+
,k∈Z可解得kπ+
≤x≤kπ+
,k∈Z
∴函数f(x)的单调减区间是[kπ+
,kπ+
],k∈Z.
| OA |
| OB |
| 3 |
| 3 |
| π |
| 6 |
(2)∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴f(x)min=-1=f(
| 7π |
| 6 |
∴a=-1
∵令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
∴函数f(x)的单调减区间是[kπ+
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查了平面向量数量积的运算,两角和与差的正弦函数公式的应用,正弦函数的单调性,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“a>b>0”是“a2>b2”成立的( )条件.
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
R表示实数集,集合M={x∈R|0<log3x<1},N={x∈R||2x-3|<1},则( )
| A、M∩N=N |
| B、M∪N=N |
| C、(∁RN)∩M=φ |
| D、(∁RM)∩N=φ |
已知i是虚数单位,m和n都是实数,且m(1+i)=7+ni,则
( )
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
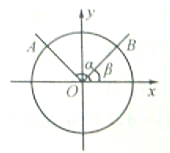 在平面直角坐标系xOy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆O的交点为A,B,则
在平面直角坐标系xOy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆O的交点为A,B,则