题目内容
9.已知动点P(x,y)在椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1上,过坐标原点的直线BC与椭圆相交,交点为B,C,点Q是三角形PBC的重心,若点A的坐标为(3,0),|${\overrightarrow{AM}}$|=1,$\overrightarrow{QM}$•$\overrightarrow{AM}$=0,则|${\overrightarrow{QM}}$|的最小值是$\frac{{\sqrt{7}}}{3}$.分析 由题意画出图形,把求|${\overrightarrow{QM}}$|的最小值转化为求|$\overrightarrow{QA}$|的最小值,再数形结合得答案.
解答 解:如图,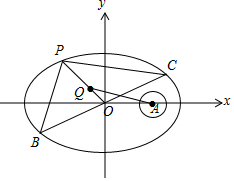
∵|${\overrightarrow{AM}}$|=1,∴M在以A(3,0)为圆心,以1为半径的圆上,
又$\overrightarrow{QM}$•$\overrightarrow{AM}$=0,∴△QMA是以∠QMA为直角的直角三角形,
∴要使|${\overrightarrow{QM}}$|最小,则|$\overrightarrow{QA}$|最小,即O、Q、A共线且Q、A在O的同侧,此时P与椭圆右顶点重合,
∵点Q是三角形PBC的重心,∴|OQ|=$\frac{1}{3}a=\frac{5}{3}$,
则$|\overrightarrow{QA}{|}_{min}=3-\frac{5}{3}=\frac{4}{3}$,∴$|\overrightarrow{QM}{|}_{min}=\sqrt{(\frac{4}{3})^{2}-{1}^{2}}=\frac{\sqrt{7}}{3}$.
故答案为:$\frac{{\sqrt{7}}}{3}$.
点评 本题考查椭圆的简单性质,考查数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.等比数列{an}中,a1=$\frac{1}{8}$,q=2,则a4与a8的等比中项是( )
| A. | ±4 | B. | 4 | C. | ±$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
14.现有16张不同的卡片,其中红、黄、蓝、绿卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张的不同抽取方法有( )
| A. | 472 种 | B. | 484 种 | C. | 232 种 | D. | 252种 |
1.已知函数f(x)=sin2x+$\sqrt{3}$(1-2sin2x).
(Ⅰ)求f(x)的单调减区间;
(Ⅱ)当x∈[-$\frac{π}{6}$,$\frac{π}{6}$]时,求f(x)的值域.
(Ⅰ)求f(x)的单调减区间;
(Ⅱ)当x∈[-$\frac{π}{6}$,$\frac{π}{6}$]时,求f(x)的值域.
18.若复数z满足z(2+3i)=1+i(其中i为虚数单位),则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |